Page 38 - 《摩擦学学报》2021年第1期

第 1 期 刘明, 等: 试样倾斜和正压力对球形压头微米划痕测试紫铜的影响 35

1.6 H s =0.956 相比锥形压头(如棱锥压头和圆锥压头)，球形压头由
于不具有几何自相似性，产生的较大压痕比较小的压
Scratch hardness, H s r /GPa 1.2 痕所涉及的塑性应变更大，有效屈服应力的增加幅度
1.4
r
[9]
也更大，因此所观察到的硬度明显增加 . 也有可能是
1.0
由于应变硬化或者位错密度随正压力和划痕深度增
0.8
[24]
大而增大导致的 . 对比图14可知，由于公式(25)中的
0.6
S v 与 S n 表示划痕过程中压头与试样在法向和竖直方
0.4 向的实时接触投影面积，其与 F v 不为线性关系，因此
0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6
θ
θ
Normal load, F v /N 得到的划痕硬度不是恒定值. 稳定后的 H 与 H 均大于
v n
r
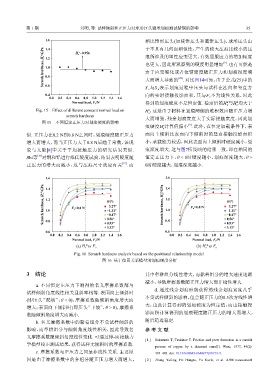
Fig. 15 Effect of different constant normal load on H ，这是由于材料在划痕两侧的堆积效应随正压力增
s
scratch hardness
大而增强，残余划痕宽度大于实际接触宽度，因此划
图 15 不同恒定正压力对划痕硬度的影响
[8]
痕硬度 H 计算值偏小 . 此外，在恒定加载条件下，表
r
s
似. 正压力在0.2 N到0.8 N之间时，划痕硬度随正压力 面向上倾斜比表面向下倾斜时的竖直接触投影面积
增大而增大，而当正压力大于0.8 N后趋于常数，该现 小，承载能力较弱，因此表面向上倾斜时硬度减小，划
象与文献[8]中关于平均接触压力的研究结果类似. 痕深度增大. 这与图7所反映的结果一致，即在相同的
[10]
Shi等 对铜和铝进行维氏硬度试验，结果表明硬度随 恒定正压力下，θ < 0时硬度越小，划痕深度越大，θ >
[12]
正压力的增大而减小，这与压痕尺寸效应有关 . 而 0时硬度越大，划痕深度越小.

1.6 1.6
Scratch hardness, H v θ /GPa 1.2 F v =0.8 N θ/(°) Scratch hardness, H n θ /GPa 1.2 F n =0.8 N θ/(°)
1.4
1.4
−3.27°
−3.27°
−1.11°
−1.11°
1.0
1.0
−0.47°
−0.47°
0.56°
0.8
0.93°
0.93°
3.12°
3.12° 0.8 0.56°
0.6 0.6
0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6
Normal load, F v /N Normal load, F v /N
θ
θ
(a) H v vs F v (b) H n vs F n
Fig. 16 Scratch hardness analysis based on the positional relationship model
图 16 基于位置关系模型的划痕硬度分析

3 结论 其中犁耕组分线性增大，而黏着组分的增大速度逐渐
减小，导致摩擦系数随正压力增大而非线性增大.
a. 不同恒定正压力下测得的名义摩擦系数都与
d. 通过残余划痕形貌获得的残余划痕宽度几乎
试样倾斜角度线性相关且斜率相等. 表面向上倾斜时
不受试样倾斜的影响，但会随正压力的0.5次方线性增
(即压头“爬坡”，θ < 0)，摩擦系数随倾斜角度增大而
大，由此计算得到的划痕硬度为恒定值，而由接触投
增大；表面向下倾斜时(即压头“下坡”，θ > 0)，摩擦系
影面积计算得到的划痕硬度随正压力的增大而增大，
数随倾斜角度增大而减小.
b. 名义摩擦系数中的黏着组分不受试样倾斜的 随后趋近稳定.
影响，而犁耕组分与倾斜角度线性相关，因此导致名 参 考 文 献
义摩擦系数随倾斜角度线性变化. 可通过球-面接触力
[ 1 ] Sakamoto T, Tsukizoe T. Friction and prow formation in a scratch
学模型校正测试结果，获得试样无倾斜时的摩擦系数.
process of copper by a diamond cone[J]. Wear, 1977, 44(2):
c. 摩擦系数与正压力之间呈非线性关系. 主要原 393–403. doi: 10.1016/0043-1648(77)90153-3.
因是由于摩擦系数中的各组分随正压力增大而增大， [ 2 ] Zhang Yafeng, He Hongtu, Yu Jiaxin, et al. AFM nanoscratch