Page 59 - 《摩擦学学报》2020年第6期

742 摩 擦 学 学 报 第 40 卷

1.2 度系数反映了转子受到径向气流力的效果，表征了气
ε=0, min ε=0, max
ε=0.1, min ε=0.1, max
1.0 ε=0.3, min ε=0.3, max 流力对密封系统刚度的影响；交叉刚度反映了转子受
ε=0.5, min ε=0.5, max 到切向气流力的大小，是促使转子涡动与失稳的主要
ε=0.7, max
ε=0.7, min
Mach number 0.6 原因；直接阻尼反映了系统阻尼作用的大小，是涡动
0.8
ε=0.9, max
ε=0.9, min
现象的抑制力，利于稳定性的提高；交叉阻尼对系统
0.4
稳定性影响较小. 式(17)中密封有效阻尼系数 C eff 是衡
0.2 量密封系统动态稳定性的重要指标，有效阻尼越大，
0 系统越稳定 [22-23] .
0 5 10 15 20 25 30 35 40 45 50 55 60 65
Axial position/mm 3.2.1 偏心率对密封刚度系数的影响

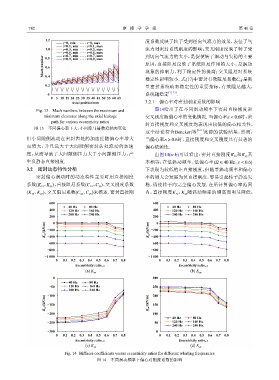
图14给出了在不同涡动频率下密封直接刚度和
Fig. 13 Mach numbers between the maximum and
minimum clearance along the axial leakage 交叉刚度随偏心率的变化情况. 当偏心率 ε < 0.6时，密
path for various eccentricity ratios
封直接刚度和交叉刚度均表现出较低的偏心相关性，
图 13 不同偏心率下大、小间隙马赫数沿轴向变化
这个结论符合Benckert等 [9-11] 此前的试验结果，然而，
但小间隙侧流动在密封齿处的加速度随偏心率增大 当偏心率 ε ⩾ 0.6时，直接刚度和交叉刚度具有显著的
而增大，并且远大于大间隙侧密封齿处流动的加速 偏心依赖性.
度，从而导致了大间隙侧压力大于小间隙侧压力，产 由图14(a~b)可以看出：密封直接刚度 K xx 和 K yy 基
，
生负静态直接刚度. 本相等，在低涡动频率、低偏心率( Ω ⩽ 40 Hz ε < 0.6)
3.2 密封动态特性分析 下表现为较低的正直接刚度，但随着涡动频率和偏心
密封偏心涡动时的动态特性主要可用直接刚度 率的增大会发展为负直接刚度，容易引起转子静态失
、
、
系数( K xx K yy )、直接阻尼系数( C xx C yy)、交叉刚度系数 稳，诱使转子向完全偏心发展. 在所计算偏心率范围
、
、
、
( K xy K yx )、交叉阻尼系数( C xy C yx )来描述. 密封直接刚 内，直接刚度 K xx K yy 随涡动频率的增高而明显降低，
600 600
40 Hz 80 Hz 40 Hz 80 Hz
400 120 Hz 160 Hz 400 120 Hz 160 Hz
200 Hz 240 Hz 200 Hz 240 Hz
200 0 200 0
K xx /(kN/m) −200 K yy /(kN/m) −200
−400
−400
−600 −600
−800 −800
−1 000 −1 000
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
Eccentricity ratio, ε Eccentricity ratio, ε
(a) K xx (b) K yy
0 300
40 Hz 80 Hz
−50 120 Hz 160 Hz 250
200 Hz 240 Hz 200
−100
K xy /(kN/m) −150 K yx /(kN/m) 150

−200 100
40 Hz 80 Hz
−250 50 120 Hz 160 Hz
200 Hz 240 Hz
−300 0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
Eccentricity ratio, ε Eccentricity ratio, ε
(c) K xy (d) K yx

Fig. 14 Stiffness coefficients versus eccentricity ratios for different whirling frequencies
图 14 不同涡动频率下偏心对刚度系数的影响