Page 57 - 《摩擦学学报》2020年第6期

740 2 000 EXP, Ertas 摩 擦 学 学 报 3 000 EXP, Ertas 第 40 卷

Average direct stiffness, K avg /(kN/m) 1 500 0 Current CFD Average direct damping, C avg /(N·s/m) 2 000 0 Current CFD

1 000
1 000
500

−500
−1 000
−2 000
−1 500
0 40 80 120 160 200 240 280 −1 000 0 40 80 120 160 200 240 280
Whirling frequency/Hz Whirling frequency/Hz
(a) Average direct stiffness, K avg 4 000 (b) Average direct damping, C avg
2 000
Cross-coupled stiffness, K xy , K yx /(kN/m) 1 000 0 Current CFD, K yx Effective damping, C eff /(N·s/m) −1 000 0 Current CFD
EXP, Ertas
EXP, Ertas
3 000
1 500
Current CFD, K xy
2 000
1 000
500
−500

−1 000
160
120
0
40
200
160
120
80
80
200
Whirling frequency/Hz 240 280 −2 000 0 40 Whirling frequency/Hz 240 280
(c) Cross-coupled stiffness, K xy , K yx (d) Effective damping, C eff

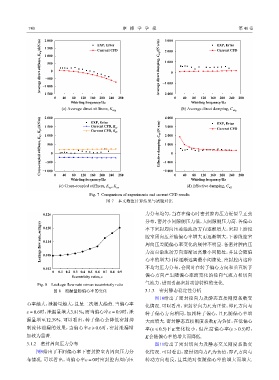
Fig. 7 Comparison of experiments and current CFD results
图 7 本文数值计算结果与试验对比
0.126 力分布均匀，当存在偏心时密封腔内压力近似呈正弦
分布，密封小间隙侧压力低，大间隙侧压力高. 各偏心
Leakage flow rate, m/(kg/s) 0.114 腔室周向压差随偏心率增大而逐渐增大，下游段腔室
0.120
率下密封周向压差沿流动方向逐渐增大，密封上游段
周向压差随偏心率变化的规律不明显. 各密封腔内压
力高点沿流动方向逐渐远离最小间隙处，并且会随偏
0.108
心率的增大同样逐渐远离最小间隙处. 密封腔内这种
不均匀压力分布，会同时在转子偏心方向和垂直转子
0.102
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
Eccentricity ratios, ε 偏心方向产生随偏心率而变化的径向气流力和切向

Fig. 8 Leakage flow rate versus eccentricity ratio 气流力，进而引起密封动静特性的变化.
图 8 泄漏量随偏心率的变化 3.1.3 密封静态稳定性分析
图10给出了密封径向力及静态直接刚度系数变
心率越大，泄漏量越大，且呈二次增大趋势. 当偏心率
化情况. 可以看出，密封径向力 F r 为正值，即 F r 方向与
ε = 0.6时，泄漏量增大3.81%；而当偏心率 ε = 0.9时，泄 转子偏心方向相同，加剧转子偏心，且 F r 随偏心率增
漏量增至12.39%. 可以看出，转子偏心会降低密封抑 大而增大. 密封静态直接刚度系数 K为负值，在低偏心
制流体泄漏的效果，当偏心率 ε ⩾ 0.6时，密封泄漏增 率( ε ⩽ 0.5)下 变化较小，但在高偏心率( ε > 0.5)时，
K
加较为显著. K会随偏心率的增大而降低.
3.1.2 密封周向压力分布 图11给出了密封切向力及静态交叉刚度系数变
图9给出了不同偏心率下密封腔室内周向压力分 化情况. 可以看出，密封切向力 F t 为负值，即 方向与
F t
布情况. 可以看出，当偏心率 ε = 0时密封腔内周向压 转动方向相反，且其绝对值随偏心率的增大而增大.