Page 60 - 《摩擦学学报》2020年第6期

第 6 期 秦鹏博, 等: 偏心迷宫密封动静特性研究 743

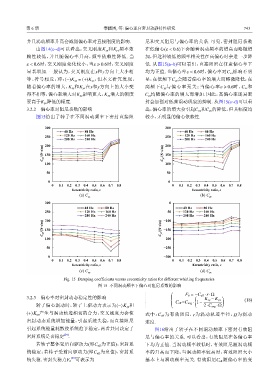
并且涡动频率升高会减弱偏心率对直接刚度的影响. 尼和交叉阻尼与偏心率的关系. 可见，密封阻尼系数
由图14(c~d)可以看出：交叉刚度 K xy 和 K yx 频率依 在低偏心( ε < 0.6)下会随着涡动频率的增高而略微增
赖性较低，并且随偏心率升高，频率依赖性降低. 当 加，但这种较低的频率相关性在高偏心时会进一步降
ε < 0.6时，交叉刚度变化较小，当 ε ⩾ 0.6时，交叉刚度 低. 从图15(a~b)可以看出，直接阻尼在任意偏心率下
显著增加. 一般认为，交叉刚度在 x和 y方向上大小相 均为正值. 当偏心率 ε < 0.6时，偏心率对 C xx 影响不明
等、符号相反，即： (−)K xy = (+)K yx ，但本文研究发现， 显，在低频下 C yy会随着偏心率的增大而略微降低，在
随着偏心率的增大， K xy 和 K yx 在 x和 y方向上的大小变 高频下 C yy与偏心率无关；当偏心率 ε ⩾ 0.6时， C xx 和
得不相等，偏心率增大对 K xy 影响更大， K xy 增大的幅度 C yy均随偏心率的增大而增加. 因此，高偏心率迷宫密
要高于 K yx 降低的幅度. 封会加强对低频涡动现象的抑制. 从图15(c~d)可以看
3.2.2 偏心率对阻尼系数的影响 出，偏心率的增大会引起 C xy 和 C yx 的降低，但其幅度均
图15给出了转子在不同涡动频率下密封直接阻 较小，无明显的偏心依赖性.

300 300
40 Hz 80 Hz 40 Hz 80 Hz
120 Hz 160 Hz 120 Hz 160 Hz
250 250
200 Hz 240 Hz 200 200 Hz 240 Hz
200
C xx /(N·s/m) 150 C yy /(N·s/m) 150

100 100

50 50
0 0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
Eccentricity ratio, ε Eccentricity ratio, ε
(a) C xx (b) C yy
300 0
40 Hz 80 Hz 40 Hz 80 Hz
250 120 Hz 160 Hz −50 120 Hz 160 Hz
200 Hz 240 Hz −100 200 Hz 240 Hz
200
C xy /(N·s/m) 150 C yx /(N·s/m) −150

100 −200

50 −250
0 −300
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
Eccentricity ratio, ε Eccentricity ratio, ε
(c) C xy (d) C yx
Fig. 15 Damping coefficients versus eccentricity ratios for different whirling frequencies
图 15 不同涡动频率下偏心对阻尼系数的影响


3.2.3 偏心率对密封动态稳定性的影响  F θ = −C eff ·r ·Ω )

(


K xy − K yx (18)
 C eff =C avg · 1−

转子偏心涡动时，转子上驱动力表示为 (−)K xy 和  2·C avg ·Ω

(+)K yx 产生与涡动轨迹相切的合力，交叉刚度力会使 式中： C eff 为有效阻尼， 为涡动轨迹半径， 为涡动
Ω
r
密封动态系统增加能量，引起系统失稳，而直接阻尼 速度.
引起系统能量耗散使系统趋于稳定，两者共同决定了 图16给出了转子在不同涡动频率下密封有效阻
[24]
密封系统是否稳定 . 尼与偏心率的关系. 可以看出，有效阻尼在各偏心率
若转子整体受后向驱动力(即 C eff 为正值)，密封系 下均为正值. 当涡动频率较低时，有效阻尼随涡动频
统稳定；若转子受前向驱动力(即 C eff 为负值)，密封系 率的升高而下降；当涡动频率较高时，有效阻尼大小
统失稳. 密封失稳力 F θ [25] 可表示为 基本上与涡动频率无关. 有效阻尼 C eff 随偏心率的变