Page 45 - 《摩擦学学报》2020年第6期

728 摩 擦 学 学 报 第 40 卷

相的运动进行描述，DPM模型考虑了相间耦合作用以
及耦合作用对离散相和连续相运动的影响，其在笛卡 8.3 Erosion rate
尔坐标系的运动方程为 [21-23] ： 8.2
8.1
g(ρ p −ρ) Maximum/[10 −6 kg/(m 2 ·s)]
∂v p 8.0
= F d (v−v p )+ + F other (1)
∂t ρ p 7.9
式 中 右 侧 F d v−v p 为 单 位 质 量 颗 粒 受 到 的 曳 力 ； 7.8 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5
)
(
g(ρ p −ρ) Grid/10 6
为重力项， F other 为其他作用力，如附加质量
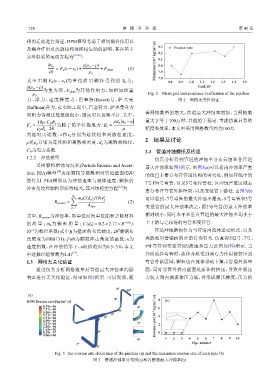
Fig. 2 Mesh grid independence verification of the pipeline
ρ p
力、浮力、速度梯度力、巴塞特(Basset)力、萨夫曼 图 2 网格无关性验证
(Saffman)升力，在实际工况中，巴塞特力、萨夫曼升力
着网格数量的增大，管道最大冲蚀率增加，当网格数
同阻力等相比数量级很小，因而可以忽略不计. 其中，

量大于等于100万时，其值趋于稳定. 考虑仿真计算的
ρd p u p −u
18µ C D R e
F d = 为粒子的单位拖曳力， R e =
ρ p d 2 24 µ 精度和效率，本文中采用网格数量约为100万.
p
为相对雷诺数， v和 分别为连续相和离散相速度，
v p
2 结果及讨论
ρ和 分别为连续相和离散相密度， 为离散相粒径，
d p
ρ p
C D 为曳力系数. 2.1 管道冲蚀磨损及机理
1.2.2 冲蚀模型 仿真分析得到管道的冲蚀率分布云图和各管道
采用颗粒磨蚀与沉积(Particle Erosion and Accre- 最大冲蚀率如图3所示. 由图3(a)可以看出冲蚀率严重
[18]
tion，PEA)模型 表征颗粒等离散相对管道壁面的冲
的位置主要分布在管道结构的突变处，例如管线中的
蚀作用. PEA模型认为冲蚀速率与流体速度、颗粒的
7号和9号弯管，以及5号变径管处，且冲蚀严重区域主
冲击角度和颗粒形状等相关，其冲蚀模型方程 为
[23]
要分布在弯管外拱壁面，以及变径管下游处. 由图3(b)
∑ m d C(d p ) f(θ)v n 可以看到，7号弯管的最大冲蚀率最高，9号弯管和5号
N p
R erosion = p (2)
A face 变径管的最大冲蚀率次之，而2号弯管的最大冲蚀率
ρ=1
式中： R erosion 为冲蚀率，即单位时间单位面积去除材料 相对较小；同时水平和垂直管道的最大冲蚀率均小于
的 质 量 ； m d 为 颗 粒 质 量 ； C (d d ) = 0.2×2.17× B −0.59 × 上下游与之相连的弯管和变径管.
#
−7
10 为粒径函数(式中 为壁面的布氏硬度，20 碳钢布 管道冲蚀磨损行为与管道内流体运动形式，以及
B
氏硬度为HBS131)； f (θ)为颗粒冲击角度的函数； n为 离散相对管壁面的冲击行为有关. 仿真得到2号、7号、
速度指数，在冲蚀情形下， n取值范围为0.5~3.0，本文 9号弯管和变径管5的流速和压力云图如图4所示. 当
[17]
中选择经验常数为2.41 . 介质流经弯管时，流体介质受到离心力作用被挤压到
1.3 网格无关化验证 弯管外拱区域，颗粒也在流体带动下撞击管道外拱壁
通过仿真分析网格数量对管道最大冲蚀率的影 面，同时弯管外拱内壁面处流体的挤压，导致外部压
响来进行无关化验证，结果如图2所示. 可以发现，随 力较大而内侧流体压力低，并形成顺压梯度，压力的

9 # 10 #
(a)
8 # 8
DPM Erosion rate/[kg/(m ·s)] (b)
2
8.19e−06 9 #
7.37e−06 6
6.56e−06 7 #
5.73e−06 6 # 4
4.91e−06 5 # Erosion rate/[10 −6 kg/(m 2 ·s)]
4.09e−06 4 #
3.27e−06 7 # 2
2.46e−06
1.64e−06
8.19e−07 3 # 0
0.00e+00
5 # 1 2 3 4 5 6 7 8 9 10
1 # Pipe number
2 #

Fig. 3 The erosion rate cloud map of the pipeline (a) and the maximum erosion rate of each pipe (b)
图 3 管道冲蚀率分布图(a)和各管道最大冲蚀率(b)