Page 56 - 《摩擦学学报》2020年第5期

第 5 期 马晓川, 等: 近场动力学框架下钢轨疲劳裂纹萌生预测的数值方法研究 611

第4步：根据公式(4)，分别计算质点的损伤指数ψ.
若损伤指数大于或等于0.5，则计算结束并输出结果； Boundary
conditions Wheel load conditions
若损伤指数小于0.5，则跳到第2步进行循环计算.
根据以上流程，采用Fortran语言，编译了相应的

计算机程序，计算程序的流程如图5所示.

Enter calculation parameters
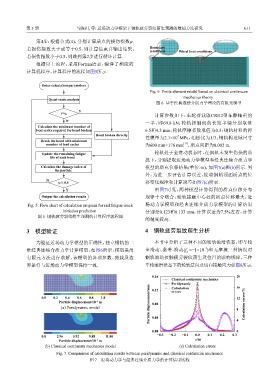
Fig. 6 Finite element model based on classical continuum
mechanics theory
Quasi-static analysis
图 6 基于经典连续介质力学理论的有限元模型
Y
计算参数如下：车轮荷载取CRH2型车静轴重的
s>s 0
N
一半，即69.8 kN；轮轨接触斑的长短半轴分别取值
Calculate the minimum number of
load cycles required for bond broken 6.5和4.5 mm；轮轨摩擦系数取值为0.3；钢轨材料的弹
Bond broken directly 5
性模量为2.1×10 MPa，泊松比为1/3；钢轨构造域尺寸
Break the bond with minimum
[17]
number of load cycles 为600 mm×176 mm ，质点间距为0.002 m.
轮轨处于全滑动状态时，在钢轨未发生伤损的前
Update the remaining fatigue
life of each bond
提下，分别提取近场动力学模型和经典连续介质力学
Calculate the damage index of 模型的质点位移结果(单位:m)，如图7(a)和(b)所示. 另
the particle
外，为进一步评估计算误差，提取钢轨顶面质点的位
N
ψ≥0.5 移变化规律和计算误差如图7(c)所示.
Y 由图7可见，两种模型计算得到的质点位移分布
Output the calculation results 规律十分吻合，轮轨接触中心处的质点位移最大，近
Fig. 5 Flow chart of calculation program for rail fatigue crack 场动力学模型和经典连续介质力学模型的计算结果
initiation prediction 分别是0.123和0.133 mm，计算误差为7.5%左右，计算
图 5 钢轨疲劳裂纹萌生预测的计算程序流程图
的精度较高.

3 模型验证 4 钢轨疲劳裂纹萌生分析

为验证近场动力学模型的正确性，建立钢轨的二 本节中分析了三种不同的轮轨滚滑状态，即车轮
−3
维经典连续介质力学计算模型，如图6所示，模型采用 全滑动、黏着-滑动(f =−1×10 )和无摩擦三种情况对
x
有限元方法进行求解，该模型的各项参数、荷载及边 钢轨滚动接触疲劳裂纹萌生及位置的影响规律，三种
界条件与近场动力学模型保持一致. 车轮滚滑状态下的轮轨法向及切向接触应力如图8所示.

0.16 20
Classical continuum mechanics
Peridynamic 16
Particle displacement/mm 0.08 Calculation errors/%
Calculation
0.12
0.0 0.2 0.4 0.6 0.8 1.0 errors 12
−3
Particle displacement/10 m
(a) Peridynamic model 0.04 8

0.00 4 0
−0.3 −0.2 −0.1 0.0 0.1 0.2 0.3
0.0 2.96 5.92 8.88 11.80
−3
Particle displacement/10 m x/m
(b) Classical continuum mechanics model (c) Calculation errors
Fig. 7 Comparison of calculation results between peridynamic and classical continuum mechanics
图 7 近场动力学与经典连续介质力学的计算结果比较