Page 137 - 《爆炸与冲击》2025年第12期

第 45 卷 郭景琪，等： 马赫反射波系在平面重/轻界面的入射加载 第 12 期

2.3 界面演化过程分析
2.2 节中对马赫反射波系的入射加载过程进行了理论求解，本节运用理论计算和数值模拟结果对界
面演化前期进行定量研究，从界面环量和速度扰动 2 个角度展开分析。2.2.1 节和 2.2.2 节中的计算结果
分别是在 TP 、IP 和 1 IP 参考系下得到的，不能直接用于评估界面演化过程，需将计算结果转换到实验室
2
2
参考系中，采用如下转换公式：
( )
® lab TP 2 TP 2 TP 2
a
v 0,1,2,3 = M 0,1,2,3 0,1,2,3 cosξ 0,1,2,3 x +sinξ 0,1,2,3 y +v TP 2
e
e
( ) (19)
= M TP 2
v TP 2 0 a 0 cosφe x +sinφe y
® lab ( )
e
a
v = M 0,0',1,4,5 0,0',1,4,5 cosξ 0,0',1,4,5 x +sinξ IP 1 e
IP 1
IP 1
0,0',1,4,5 0,0',1,4,5 y +v IP 1
(20)
IP 1
= −M a 0 e y
0
v IP 1
® lab ( )
e
v = M 0,0',3,6,7 0,0',3,6,7 cosξ 0,0',3,6,7 x +sinξ IP 2 e
IP 2
IP 2
a
0,0',3,6,7 0,0',3,6,7 y +v IP 2
(21)
IP 2
= M a 0 e y
0
v IP 2
式中：v lab 为实验室坐标系下的各流场区域速度矢量， v TP 2 、 v IP 1 和 v IP 2 分别为参考点 TP 、IP 和 1 IP 的运动
2
2
速度，上标 TP 、IP 和 1 IP 表示在该参考系下的物理量，ξ 为各流场区域中气流方向与 x 轴的夹角，e 和
2
x
2
e 为单位基矢量，运用转换后速度计算界面环量和速度扰动。
y

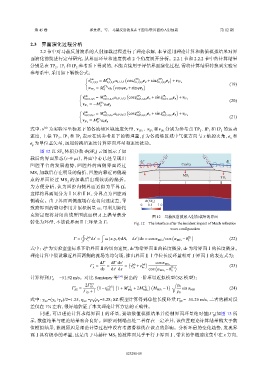
图 12 以 SF 体积分数 Φ(SF ) 云图展示了加
6
6
载后的界面形态（t=9 μs），界面中心已经呈现出
dΓ dΓ
凹腔平台的发展趋势，凹腔外的两侧界面经过 Cavity
MS 加载后存在明显的偏折，凹腔内靠近两侧端
1
MS 3
点的界面经过 MS 的加载后出现较弱的偏折。 TS 1
2
Ⅰ Ⅱ
为方便分析，认为凹腔内侧界面近似为平界面，
这样将界面划分为Ⅰ区和Ⅱ区，分界点为凹腔两
侧端点。由于界面两侧流场存在切向速度差，导 Φ(SF 6 )
0 0.5 1.0
致跨界面的剪切作用并累积涡量 ω，可利用斯托
克斯定理将封闭曲线所围成面积 A 上涡量积分 图 12 马赫反射波系入射加载后的界面
转化为环量，不妨设界面Ⅱ上环量为 Γ： Fig. 12 The interface after the incident impact of Mach reflection
wave configuration
z w ( )
lab
Γ = v ds = ω(x,y,t)dA, ds /ds = cosα MS 1 /cos α MS 1 −θ IP 1 (22)
′
′
5
τ
v lab 为实验室坐标系下沿界面Ⅱ的切向速度，ds'为沿界面Ⅱ的长度微分，ds 为沿界面Ⅰ的长度微分。
式中： τ
理论计算中假设靠近界面两侧的流场为均匀场，推出界面Ⅱ上单位长度环量相对于界面Ⅰ的表达式为：
dΓ dΓ ds ′ ( )
lab
Γ = = = v +v lab ( cosα MS 1 ) (23)
′
A
5τ
4τ
ds ds ds cos α MS 1 −θ IP 1
′
5
Γ ′ = −51.92 m/s。对比 Samtaney 等 [34] 提出的一阶环量近似模型（SZ 模型）：
A
计算得到
2Γ 0.5 ( )( )( ) … p 0
′
Γ = SZ 1−η −0.5 1+ M −1 +2M −2 −1 (24)
SZ SZ MS 1 MS 1 M MS 1 sinα MS 1
Γ SZ +1 ρ 0
式中：γ =(γ +γ )/2=1.25，η =ρ /ρ =5.28；SZ 模型计算得到单位长度环量 Γ ′ SZ =−51.25 m/s，二者的相对误
SZ
0'
0
SZ
0
0'
差仅在 1% 左右，很好地佐证了本文理论计算方法的正确性。
同理，可以理论计算求得界面Ⅰ的环量，提取数值模拟结果并绘制界面环量绝对值|Γ' |如图 13 所
N
示，数值结果与理论结果吻合良好。凹腔两侧端点处二者存在一定差异，该位置理论计算结果稍大于数
值模拟结果，推测原因是理论计算过程中没有考虑滑移线在该点的影响。分析环量的变化趋势，发现界
面Ⅰ具有极小的环量，这是由于马赫杆 MS 的波阵面几乎平行于界面Ⅰ，带来的伴随速度集中在 x 方向，
2
123201-10