Page 115 - 《爆炸与冲击》2025年第12期

第 45 卷 汪 腾，等： 基于不同本构模型下的白砂岩动态力学性能仿真分析与实验验证 第 12 期

p crush = f c /3, µ crush = p crush /K, µ lock = ρ c /ρ 0 −1, ρ c = ρ 0 /(1−α 0 ) (14)

式中：ρ 为岩石的压实密度。 18
c
Experimental data
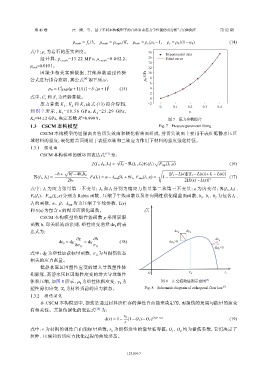
经 计 算 ， p =13.22 MPa， μ =0.002 2， 16 Fitted curve
crush crush
14
μ lock =0.010 1。 12
因缺少相关实验数据，其他参数通过经验 10
[4]
公式进行拟合获取，其公式 如下所示： p H /GPa 8
6
2
p H = C ρ 0 µ(µ+1)/[(1−S 1 )µ+1] 2 (15) 4
1
2
式中：C 和 1 S 为经验常数。 0
1
压力常数 K 、K 和 2 K 由式 (13) 拟合得到， −2
3
1
0 0.1 0.2 0.3 0.4
如 图 7 所 示 ， K 1 = 1 8 . 5 6 G P a ， K 2 = 2 5 . 2 9 G P a ， µ
K =94.12 GPa，决定系数 R =0.999 9。
2
3 图 7 压力参数拟合
1.3 CSCM 本构模型 Fig. 7 Pressure parameter fitting
CSCM 本构模型的屈服面由剪切失效面和硬化帽盖面组成，剪切失效面主要用于表征低静水压区
域材料的强度，硬化帽盖面则用于表征双轴和三轴应力作用下材料的强度强化特征。
1.3.1 强度面
CSCM 本构模型的破坏面表达式 [17] 为：
√ √
f(I 1 , J 2 , J 3 ) = J 2 −ℜ(I 1 , J 3 )F f (I 1 ) F cap (I 1 ,κ) (16)
√
2
−b+ b −4b 2 b 0 [I 1 − L(κ)][|I 1 − L(κ)|+ I 1 − L(κ)]
1
ℜ(I 1 , J 3 ) = , F f (I 1 ) = α−λ exp βI 1 +θI 1 , F cap (I 1 ,κ) = 1− (17)
2b 2 2[X(κ)− L(κ)] 2
J 3 分别为偏应力张量第二和第三不变量；κ ℜ(I 1 , J 3 ) 、
式中： I 1 为应力张量第一不变量； J 2 和 为内变量；
F f (I 1 )、F cap (I 1 ,κ) 分别为 Rubin 函数、压缩子午线函数以及各向同性强化帽盖面函数，b 、b 、b 为包含 I 1 、
2
0 1
L(κ)
J 3 的函数， α、β、λ exp 均为压缩子午线参数，
X(κ) 为包含 κ 的帽盖面演化函数。
和 J 2
CSCM 本构模型的塑性势函数 g 采用屈服
函数 h，即关联流动法则，塑性应变增量 dε p 的表
达式为： dε p dγ p
∂g ∂h dε p
dε p = dχ = dχ (18) dµ p >0
∂σ i j σ ij
dµ p <0
σ ij 为与损伤状态
式中： dχ 为塑性加载标量函数，
相关的应力张量。
低静水压区因塑性应变的增大导致塑性体
积膨胀，高静水压区因塑性应变的增大导致塑性 O X 0 I 1
体积压缩，如图 8 所示， µ p 为塑性体积应变， γ p 为 图 8 正交流动法则示意图 [7]
塑性剪切应变，X 为材料当前的应力状态。 Fig. 8 Schematic diagram of orthogonal flow law [7]
0
1.3.2 损伤演化
在 CSCM 本构模型中，损伤是通过材料所贮存的弹性自由能来决定的，而损伤的发展与能量的演变
有相关性。其损伤演化的表达式 [18] 为：

r 0 O 2 (r−r 0 )
d(r) = 1− (1−O 1 )−O 1 e (19)
r
式中：r 为材料的弹性自由能标量函数；r 为损伤发生的能量临界值；O 、O 均为损伤参数，它们决定了
2
0
1
拉伸、压缩和剪切应力软化过程的曲线形态。

123104-7