Page 119 - 《爆炸与冲击》2025年第12期

第 45 卷 汪 腾，等： 基于不同本构模型下的白砂岩动态力学性能仿真分析与实验验证 第 12 期

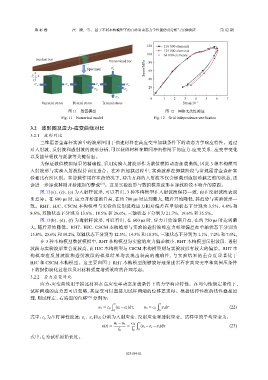
120 216 000 elements
125 000 elements
100 64 000 elements
Incident bar Transmitted bar 80
Specimen σ z Stress/MPa 60
y z x
O 40
σ x σ x σ x σ x
20
σ y σ y
0 1 2 3 4 5 6 7
σ z
Uniaxial stress Biaxial stress Triaxial stress Strain/10 −3
图 11 数值模型 图 12 网格无关性验证
Fig. 11 Numerical model Fig. 12 Grid independence verification

3.2 波形图及应力-应变曲线对比
3.2.1 波形对比
三维霍普金森杆实验中的波形图用于描述材料在高应变率加载条件下的动态力学响应特性。通过
对入射波、反射波和透射波的波形分析，可以获得材料在瞬间冲击作用下的应力-应变关系、应变率变化
以及能量吸收与耗散等关键信息。
为保证数值模拟结果的精确性，采用实验入射波形作为数值模拟动态加载曲线，因此 3 种本构模型
入射波形与实验入射波保持高度重合。在冲击加载过程中，实验波形在卸载阶段与常规霍普金森杆实
验相比有所区别。在静载作用存在的情况下，冲击方向的入射波不仅会卸载到施加动载之前的状态，还
会进一步卸载掉刚开始施加的静载 [21] 。这是实验波形与数值模拟波形在卸载阶段不吻合的原因。
图 13(a)、(c)、(e) 为入射杆波形，可以看出，3 种本构模型在入射波段保持一致，而在反射波段表现
出差异。在 600 μs 时，应力开始逐渐升高，在约 700 μs 时达到最大，随后开始降低，其趋势与实验波形一

致。RHT、HJC、CSCM 本构模型与实验的反射波峰应力相对偏差在单轴状态下分别为 3.5%、4.4% 和
8.6%，双轴状态下分别为 13.6%、18.5% 和 26.6%，三轴状态下分别为 21.7%、19.6% 和 35.5%。
图 13(b)、(d)、(f) 为透射杆波形，可以看出，在 600 μs 时，应力开始逐渐升高，在约 750 μs 时达到最
大，随后开始降低。RHT、HJC、CSCM 本构模型与实验的透射波峰应力相对偏差在单轴状态下分别为
15.8%、25.6% 和 19.2%，双轴状态下分别为 12.5%、14.3% 和 18.5%，三轴状态下分别为 1.1%、7.2% 和 7.6%。
在 3 种本构模型数值模拟中，RHT 本构模型与实验的应力偏差较小，RHT 本构模型反射波段、透射
波段与实验波形重合度较高，而 HJC 本构模型与 CSCM 本构模型则与实验波形有较大的偏差。RHT 本
构 模 型 在 反 射 波 段 和 透 射 波 段 的 模 拟 结 果 均 表 现 出 较 高 的 准 确 性 ， 与 实 验 结 果 的 重 合 度 显 著 优 于
HJC 和 CSCM 本构模型。这主要归因于 RHT 本构模型能够较好地描述岩石在高应变率和高围压条件
下的损伤演化过程以及对材料强度增强效应的合理考虑。
3.2.2 应力应变对比
应力-应变曲线用于描述材料在高应变率动态加载条件下的力学响应特性。在均匀性假定条件下，
试样两端的应力差可以忽略，其应变可以直接用试样两端的位移差求得。根据线弹性波的线性叠加原
理，则试样左、右端面的位移 [22] 分别为：
w w
t t
(ε i −ε r )dτ, ε t dτ (22)
u 1 = c 0 u 2 = c 0
0 0
0 ε t 分别为入射应变、反射应变和透射应变。试样中的平均应变为：
式中：c 为压杆弹性波速； ε i 、 ε r 和
w t
u 1 −u 2 c 0
ε(t) = = (ε i −ε r −ε t )dτ (23)
l 0 l 0 0
式中：l 为试样原始长度。
0
123104-11