Page 121 - 《爆炸与冲击》2025年第12期

第 45 卷 汪 腾，等： 基于不同本构模型下的白砂岩动态力学性能仿真分析与实验验证 第 12 期

w t
2c 0 A 0 E 0
ε = − ε r dτ, σ = ε t (27)
l 0 0 2A s
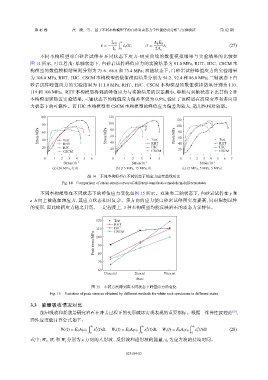
不同本构模型对白砂岩试件在不同状态下应力-应变曲线的数值模拟结果与实验结果的比较如
图 14 所示，可以看出：单轴状态下，白砂岩试件峰值应力的实验结果为 91.0 MPa，RHT、HJC、CSCM 本
构模型的数值模拟结果则分别为 75.6、66.8 和 73.4 MPa；双轴状态下，白砂岩试件峰值应力的实验结果
为 108.0 MPa，RHT、HJC、CSCM 本构模型的数值模拟结果分别为 94.2、92.4 和 86.8 MPa；三轴状态下白
砂岩试件峰值应力的实验结果为 111.0 MPa，RHT、HJC、CSCM 本构模型的数值模拟结果分别为 110、
119 和 100 MPa。RHT 本构模型得到的峰值应力与实验结果的误差最小，单轴与双轴状态下比其他 2 种
本构模型更贴近实验结果，三轴状态下的峰值应力偏差率仅为 0.9%，验证了该模型在高应变率和多向应
力状态下的可靠性。而 HJC 本构模型和 CSCM 本构模型的峰值应力偏差均较大，适用性相对较弱。

100 120

120
80 100 100
80
Stress/MPa 60 Test Stress/MPa 60 Test Stress/MPa 80 Test
60
40
HJC
HJC
HJC
20 RHT 40 RHT 40 RHT
20
20
CSCM CSCM CSCM
0 1 2 3 4 5 6 0 1 2 3 4 5 0 1 2 3 4 5 6 7
Strain/10 −3 Strain/10 −3 Strain/10 −3
(a) (20 MPa, 0, 0) (b) (15 MPa, 15 MPa, 0) (c) (5 MPa, 5 MPa, 5 MPa)
图 14 不同本构模型在不同状态下的应力应变曲线对比
Fig. 14 Comparison of stress-strain curves of different constitutive models in different states
不同本构模型在不同状态下的峰值应力变化如图 15 所示。双轴和三轴状态下，白砂岩试件在 y 和
z 方向上被施加预应力，其应力状态相对复杂。多方向的应力使白砂岩试件密实度提高，同时限制试件
的变形，因此峰值应力随之升高。一定程度上，3 种本构模型均能反映岩石的动态力学特征。

120 Test
RHT
110 HJC
CSCM
Peak stress/MPa 100
90

80
70
60
Uniaxial Biaxial Triaxial
State

图 15 不同方法得到在不同状态下峰值应力的变化
Fig. 15 Variation of peak stresses obtained by different methods for white rock specimens in different states

3.3 能量吸收情况对比
能量吸收和耗散是研究岩石在冲击过程下的变形破坏宏观表现的重要指标。根据一维弹性波理论 ，
[23]
弹性应变能计算公式如下：
w w w
t 0 2 t 0 2 t 0 2
ε (t)dt, ε (t)dt, ε (t)dt (28)
W i (t) = E 0 A 0 c 0 i W r (t) = E 0 A 0 c 0 r W t (t) = E 0 A 0 c 0 t
0 0 0
式中：W 、W 和 r W 分别为 x 方向的入射波、反射波和透射波的能量，t 为应力波的持续时间。
t
0
i
123104-13