Page 114 - 《爆炸与冲击》2025年第12期

第 45 卷 汪 腾，等： 基于不同本构模型下的白砂岩动态力学性能仿真分析与实验验证 第 12 期

∗
σ = A H + B H p ∗N H (9)
A H 可通过三轴受压实验数据获取，具体公式为：
参数
(10)
A H = c H / f c
c H 依据 Mohr-Coulomb 定律确定，具体表述为：
式中： c H 为内聚力。
σ 1 = σ 3 (1+sinθ)/(1−sinθ)+2c H cosθ/(1−sinθ) (11)
式中：θ 为内摩擦角。
表 2 不同围压下的强度
静态压缩数据由 Hoek-Brown 准则经验公式
Table 2 Strengths at different confining prestresses
即式 (7) 获得，因此不同围压下的强度如表 2 所
σ 2 =σ 3 /MPa σ 1 /MPa
示。将表 2 中的数据通过式 (11) 进行拟合，拟合
0 39.67
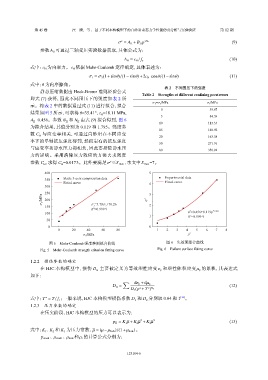
结果如图 5 所示，可求得 θ=35.41°，c =18.11 MPa，
H
5 84.59
A =0.456。参数 B 和 H N 由式 (9) 拟合得到，图 6
H
H
10 115.33
为拟合结果，其值分别为 0.119 和 1.795。强度参
15 140.92
数 C 与应变率相关，可通过白砂岩在不同应变
H
20 163.58
率下的单轴抗压强度得到，然而岩石的抗压强度
50 271.76
与应变率和静水压力都相关，因此要排除静水压
80 358.82
力的影响。采用消除压力效应的方法去求强度
参数 C ，求得 C =0.017 3。此外要满足 σ ≤S max ，本文中 S max =7。
∗
H H
400 5
350 Static 3-axis compression data Experimental data
Fitted curve 4 Fitted curve
300
250 3
σ 1 /MPa 200 σ *
150 σ 1 =3.79σ 3 +70.26 2
R =0.999 9
2
*
100 σ =0.456+0.119p *1.795
1 R =0.999 9
2
50
0 0
0 20 40 60 80 1 2 3 4 5 6 7 8
σ 3 /MPa p *
图 5 Mohr-Coulomb 强度准则拟合曲线 图 6 失效面拟合曲线
Fig. 5 Mohr-Coulomb strength criterion fitting curve Fig. 6 Failure surface fitting curve

1.2.2 损伤参数的确定
在 HJC 本构模型中，损伤 D 主要被定义为等效塑性应变 ε p 和塑性体积应变 µ p 的累积，其表达式
H
如下：
∑
dε p +dµ p
D H = (12)
D 1 (p +T )
∗
∗ D 2
[16]
T = T/ f c ；一般来说，HJC 本构模型损伤系数 D 和 1 D 分别取 0.04 和 1 。
∗
2
式中：
1.2.3 压力参数的确定
在压实阶段，HJC 本构模型的压力可以表示为：
2
p H = K 1 µ+ K 2 µ + K 3 µ 3 (13)
式中：K 、K 和 2 K 为压力常数， µ = (µ−µ lock )/(1+µ lock ) 。
3
1
ρ c 的计算公式分别为：
p crush 、 µ crush 、 µ lock 和
123104-6