Page 113 - 《爆炸与冲击》2025年第12期

第 45 卷 汪 腾，等： 基于不同本构模型下的白砂岩动态力学性能仿真分析与实验验证 第 12 期

Å ã 1/2
σ 3
σ 1 = σ 3 + f c 24 +1 (7)
f c
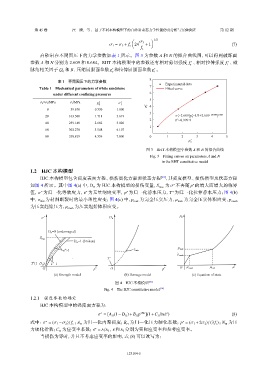
白砂岩在不同围压下的力学参数如表 1 所示。图 3 为参数 A 和 N 的拟合曲线图，可以得到破坏面
参数 A 和 N 分别为 2.609 和 0.684。RHT 本构模型中的参数还有相对剪切强度 f s ∗ 、相对拉伸强度 f t ∗ 、磁
脉角相关因子 Q 和 0 B、压缩屈服面参数 g ∗ c 和拉伸屈服面参数 g ∗ t 。

8
表 1 不同围压下的力学参数
7 Experimental data
Table 1 Mechanical parameters of white sandstone Fitted curve
6
under different confining pressures
5
σ 2 =σ 3 /MPa σ 1 /MPa p ∗ σ ∗
0 f f
σ * 4
0 39.670 0.330 1.000
3
)
*
*
20 163.580 1.711 3.619 σ f =2.609(p 0 −1/3+2.609 −1/0.684 0.684
2 R =0.999 9
2
40 239.140 2.682 5.020
1
60 302.278 3.548 6.107
80 358.819 4.359 7.000 0 1 2 3 4 5
*
p 0
图 3 RHT 本构模型中参数 A 和 N 的拟合曲线
Fig. 3 Fitting curves on parameters A and N
in the RHT constitutive model
1.2 HJC 本构模型
HJC 本构模型包含强度表面方程、损伤演化方程和状态方程 [16] ，其强度模型、损伤模型及状态方程
如图 4 所示。其中图 4(a) 中，D 为 H HJC 本构模型的损伤变量，S ma x 为 σ ∗ 不再随 p ∗ 的增大而增大的临界
σ ∗ ˙ ε ∗ p ∗ T ∗ 为归一化拉伸静水压力；图 4(b)
值， 为归一化等效应力， 为无量纲应变率， 为归一化静水压力，
ε min 为材料断裂时的最小塑性应变；图 4(c) 中，p k 为完全压实压力，μ k 为完全压实体积应变，p
loc loc crush
中，
为压实起始压力，μ crus h 为压实起始体积应变。

σ * D H p H

D H =0 (undamaged)
S max
D H =1 (broken)
*
ε >1 ε min p lock
p crush
T *
T (1−D H ) ε =1
*
*
O p * O p * O µ crush µ lock µ
(a) Strength model (b) Damage model (c) Equation of state
图 4 HJC 本构模型 [16]
Fig. 4 The HJC constitutive model [16]
1.2.1 强度参数的确定
HJC 本构模型中的强度面方程为：
∗
σ = [A H (1− D H )+ B H p ∗N H ](1+C H ln ˙ε ) (8)
∗
∗ H H p = (σ 1 +2σ 2 )/(3 f c ) ；N 为压
H
∗
式中： σ = (σ 1 −σ 2 )/ f c ；A 为归一化内聚强度；B 为归一化压力硬化系数；
H ∗ ˙ ε 0 分别为实际应变率和参考应变率。
力硬化指数；C 为应变率系数； ˙ ε = ˙ε/˙ε 0 ˙ε 和
，
当损伤为零时，并且不考虑应变率的影响，式 (8) 可以改写为：
123104-5