Page 21 - 《爆炸与冲击》2025年第9期

第 45 卷 刘 江，等： 有限长锥体诱导的斜爆轰波非定常结构的数值研究 第 9 期

的单步不可逆反应 [19, 26] 。质量总能量和反应速率分别满足：

2
p u +v 2
e = + −λq (7)
(γ −1)ρ 2
Å ã
−E a
ω = k(1−λ)exp (8)
RT
式中：γ、k、E 、R 和 q 分别为比热比、指前因子、活化能、气体常数和反应热，T 为温度。T 满足理想气体
a
状态方程：
p
T = (9)
ρR

1.2 计算方法

控制方程的数值求解是基于 OpenFOAM 平 y
台的有限体积法，并利用 OpenFOAM 中的轴对 Outflow
x
称网格补充控制方程的轴对称项（尖锥具有轴对
称特点）。控制方程中的对流项采用 Kurganov-
Noelle-Petrova (KNP) 二阶中心迎风格式 [27] ，化学
反 应 源 项 采 用 半 隐 式 B u l r s c h - S t ö e r 方 法 [ 2 8 ]
Inflow
（OpenFOAM 中的 SIBS 算法），时间项采用三阶
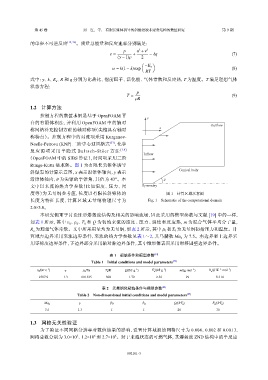
Runge-Kutta 法求解。图 1 为有限长尖锥体诱导
Conical body
斜爆轰的计算示意图，x 表示沿锥体轴向，y 表示
沿锥体径向，θ 为尖锥的半锥角，其值为 43°。本 θ
文中以来流的热力学参数（比如温度、压力、密 Symmetry
度等）为无量纲参考值，长度以有限长斜锥体的 图 1 计算区域示意图
长度为特征长度，计算区域无量纲物理尺寸为 Fig. 1 Schematic of the computational domain
2.0×3.0。
本研究侧重于讨论锥形爆轰波结构及相关的影响流场，因此采用的模型参数与文献 [19] 中的一样，
如表 1 所示，其中 v 、p 、T 和 0 Q 为初始来流的速度、压力、温度和反应热，m 为混合气体平均分子量，
0 0
R 为理想气体常数。文中所采用量均为无量纲，如表 2 所示，其中 ¯ p 0 和 T 0 为无量纲初始压力和温度。计
¯
u
算域左边界采用来流边界条件，来流的热力学参数见表 1～2，其马赫数 Ma 为 0 7.5。右边界和上边界采
用零梯度边界条件，下边界部分采用轴对称边界条件，其中锥形体表面采用滑移固壁边界条件。

表 1 初始条件和模型参数 [19]
Table 1 Initial conditions and model parameters [19]
−1
−1
−1
−1
−1
−1
v 0 /(m·s ) γ p 0 /Pa T 0 /K Q/(kJ·g ) E a /(kJ·g ) m/(g·mol ) R u /(J·K ·mol )
2507.9 1.3 101 325 300 1.72 2.58 29 8.314

表 2 无量纲化初始条件与模型参数 [19]
Table 2 Non-dimensional initial conditions and model parameters [19]
γ Q/(RT 0 ) E a /(RT 0 )
Ma 0 ¯ p 0 ¯ T 0
7.5 1.3 1 1 20 30
1.3 网格无关性验证
为了验证不同网格分辨率对数值结果的影响，设置计算域初始网格尺寸为 0.004、0.002 和 0.001 3，
网格总数分别为 3.0×10 、1.2×10 和 6 2.7×10 。对于来流状态的可燃气体，其爆轰波 ZND 结构中的半反应
5
6

092101-3