Page 62 - 《爆炸与冲击》2025年第6期

第 45 卷 胡学龙，等： 考虑动态拉压比影响的岩石损伤本构模型 第 6 期

根据以上计算流程，通过 LS-DYNA 的用户材料自定义接口 Umat，采用 Fortran 语言对本构模型的
求解进行编程，并把新生成的求解器导入 LS-DYNA 软件中。

3 模型验证

一个模型的正确与否需要通过试验进行验证，在该部分通过岩石的单轴和三轴压缩试验、单轴拉伸
试验和弹道试验对本文所建立的模型进行验证。

3.1 岩石压缩试验
Wawersik 等 [33] 对田纳西大理石进行了一系列的单轴和三轴压缩试验。田纳西大理岩的基本物理
力学参数如下：密度 ρ=2 680 kg/m ，弹性模量 E=71.91 GPa，泊松比 υ=0.20，单轴抗压强度 σ =130 MPa，单
3
c
轴抗拉强度 σ =36.65 MPa。数值模拟中大理岩有限元模型与试验中的大理岩试件形状和尺寸相同，即形
t
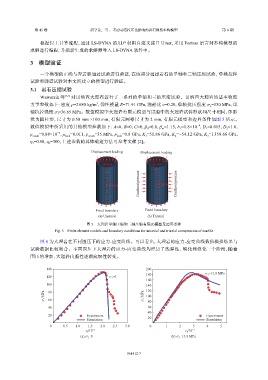
∅ 50 mm ×100 mm，有限元网格尺寸为 2 mm，有限元模型和边界条件如图 所示。
状为圆柱形，尺寸为 5
数值模拟中所采用的其他模型参数如下：A=0，B=0，C=0，β =0.8，β =1.15，b =1.8×10 ，D =0.015，D =1.0，
−4
m
2
0
1
1
−3
μ crush =0.88×10 ，μ lock =0.011，p crush =35 MPa，p lock =0.8 GPa，K =51.86 GPa，K =−54.12 GPa，K =1 359.66 GPa，
1
3
2
η =0.98，η =300，上述参数的具体确定方法可参考文献 [2]。
1
2
Displacement loading Displacement loading

50 mm 50 mm
Confined pressure 100 mm Confined pressure
100 mm

Fixed boundary Fixed boundary
(a) Uniaxial (b) Triaxial

图 5 大理岩单轴压缩和三轴压缩有限元模型及边界条件
Fig. 5 Finite element models and boundary conditions for uniaxial and triaxial compression of marble
图 6 为大理岩在不同围压下的应力-应变曲线。可以看出，大理岩的应力-应变曲线数值模拟结果与
试验数据比较吻合。不同围压下大理岩的应力-应变曲线均经历了线弹性、硬化和软化三个阶段；随着
围压的增加，大理岩由脆性逐渐向韧性转变。

140 200
180 σ 3 =13.8 MPa
120 σ 3 =0
160
100 140
σ t /MPa 80 σ t /MPa 120
100
60
80
40 60
40
20 Experiment Experiment
Simulation 20 Simulation
0 0.5 1.0 1.5 2.0 2.5 3.0 0 1 2 3 4 5
ε t /10 −3 ε t /10 −3
(a) σ 3 =0 (b) σ 3 =13.8 MPa

σ 061412-7 σ

σ σ

ε −3 ε −3
σ σ