Page 59 - 《爆炸与冲击》2025年第6期

第 45 卷 胡学龙，等： 考虑动态拉压比影响的岩石损伤本构模型 第 6 期

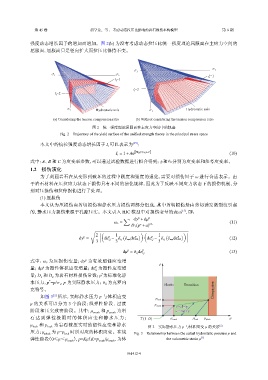
强度动态增长因子的增加而增加。图 2(b) 为没有考虑动态拉压比统一强度理论屈服面在主应力空间的
屈服面，屈服面只是径向扩大而拉压比保持不变。

σ 2
σ 1
σ 1 σ 2 I t =1
I t =1
I t =2
I t =2

σ 3 Hydrostatic axis σ 3 Hydrostatic axis
(a) Considering the tension compression ratio (b) Without considering the tension compression ratio

图 2 统一强度理论屈服面在主应力空间中的轨迹
Fig. 2 Trajectory of the yield surface of the unified strength theory in the principal stress space
本文中的抗拉强度动态增长因子 I 可以表示为 [27] ：
t
I t = 1+ Ae [ Blg(˙ε/˙ε 0 )−C] (10)
式中：A、B 和 C 为应变率参数，可以通过试验数据进行拟合得到； ˙ ε 和 ˙ ε 0 分别为应变率和参考应变率。

1.2 损伤演化
为了刻画岩石在从变形到破坏的过程中刚度和强度的退化，需要对损伤因子 ω 进行合适表示。由
于岩石材料在压拉应力状态下损伤具有不同的演化规律，因此为了反映不同应力状态下的损伤机制，分
别对压损伤和拉伸损伤进行了处理。
(1) 压损伤
本文认为压损伤由剪切损伤和静水压力损伤两部分组成，其中剪切损伤是由剪切诱发微裂纹引起
的，静水压力损伤来源于孔隙压实。本文引入 HJC 模型中对损伤变量的表示 ，即：
[5]
dγ +dµ
∑ p p
ω c = (11)
D 1 (p +a) D 2
∗

ïÅ ãÅ ãò
2 1 ( ) 1 ( )
p
p
p
p
p
dγ = dε ij − δ ij δ mn dεmn dε ij − δ ij δ mn dεmn (12)
3 3 3
p p
dµ = δ ij dε ij (13)

dγ p 为有效塑性应变增
p
式中： ω c 为压损伤变量；
p
dµ p dε i j 为塑性应变增
量； 为塑性体积应变增量；
量；D 和 1 D 为岩石材料损伤常数；p 为标准化静
*
2
*
水压力，p =p/σ ，p 为实际静水压力； δ ij 为克罗内 Elastic Transition
c
克符号。 Compaction
如图 3 [5] 所示，实际静水压力 p 与体积应变
p lock
μ 的关系可以分为 3 个阶段：线弹性阶段、过渡 p crush Loading-
Loading-
unloading
阶段和压实致密阶段。其中：μ crus h 和 p crus h 为岩 unloading
石 达 到 弹 性 极 限 时 的 体 积 应 变 和 静 水 压 力 ； T (1−D) µ crush µ lock µ plock µ
μ loc k 和 p loc k 为岩石被压实时的塑性应变和静水 图 3 实际静水压力 p 与体积应变 μ 的关系 [5]
压力；μ ploc k 为 p=p loc k 时所对应的体积应变。在线 Fig. 3 Relationship between the actual hydrostatic pressure p and
弹性阶段（0≤μ＜μ ）, p=Kμ（K=p /μ ，为体 the volumetric strain μ [5]
crush crush crush
061412-4