Page 53 - 《真空与低温》2025年第4期
P. 53
468 真空与低温 第 31 卷 第 4 期
1.0 1.4
1.2
0.8
1.0
速度/(m·s -1 ) 0.6 速度/(m·s -1 ) 0.8
0.4 0.6
0.4
0.2
0.2
0 0
0 2.5 5.0 7.5 10.0 12.5 15.0 0 2.5 5.0 7.5 10.0 12.5 15.0
通道距离/mm 通道距离/mm
(a)热流密度为 5 kW/m 2 (b)热流密度为 10 kW/m 2
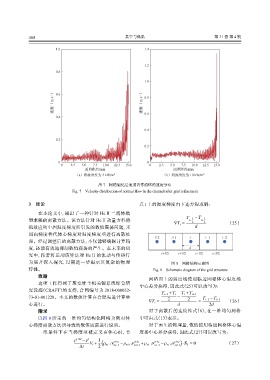
图 7 网格细化后通道内常流体的速度分布
Fig. 7 Velocity distribution of normal flow in the channel after grid refinement
3 结论 点 i 上的温度梯度由下述方程求解:
在本论文中,提出了一种针对 He II 二流体模
T 1 −T 1
型求解的离散方法。该方法针对 He II 动量方程热 i− i+
∇T i = 2 2 (25)
机效应项中因温度梯度所引发的数值震荡问题,采 d
用面梯度替代体心梯度对温度梯度项进行离散处
i+2 i+1 i i−1 i−2
理。经过调整后的离散方法,不仅能够确保计算精
度,还能有效地抑制数值震荡的产生。在未来的研 d
究中,作者将运用该算法对 He II 的流动与传热行 i+3/2 i+1/2 i−1/2 i−3/2
为展开深入探究,以期进一步揭示其复杂的物理 图 8 网格结构示意图
特性。 Fig. 8 Schematic diagram of the grid structure
致谢
网格面上的温度场使用临近网格体心温度场
这项工作得到了聚变堆主机关键系统综合研
中心差分获得,因此式(25)可以改写为:
究设施(CRAFT)的支持,合同编号为 2018-000052-
T i−1 +T i T i +T i+1
73-01-001228。本文的数值计算在合肥先进计算中 −
∇T i = 2 2 = T i−1 −T i+1 (26)
心进行。 d 2d
附录 对于离散后的连续性式(6),在一维均匀网格
以图 8 所示的一维均匀结构化网格为例对体 中可由式(13)表示。
心梯度离散方法所导致的数值震荡进行说明。 对于面上的物理量,依然使用临近网格体心温
一维条件下在当梯度项被定义在体心时,节 度场中心差分获得,因此式(27)可以改写为:
ρ t+∆t −ρ t 1 ( )
V i + ρ n,i−1 v t+∆t −ρ n,i+1 v t+∆t +ρ s,i−1 v t+∆t −ρ s,i+1 v t+∆t ·S f = 0 (27)
∆t 2 n,i−1 n,i+1 s,i−1 s,i+1