Page 172 - 《振动工程学报》2025年第9期

2102 振 动 工 程 学 报 第 38 卷

取转子轴颈表面位移场，即得由于转子热膨胀对于 ( )
y i
Φ i = arctan （25）
轴承油膜厚度的修正量 h t 。 x i
y y 式中，i 表示第 为节
T
T
e
f = B Dε 0 dv = B Dα∆Tdv （20） i 个节点；F n 为动态不平衡力；m
T
v v 点质量。
式中，ε 0 表示由温度引起的热应变。依据线性热应
力理论，微元体的总应变由两部分叠加而成：一是由 2.4 轴颈热应力计算结果
于材料的热胀冷缩特性，温度变化引起的物体应变；
基于上述理论分析，可以对转子轴颈热应力进
另一部分是由于应力引起的，如下式所示：
行瞬态仿真计算。

 1 [ ( )]
 ε x = σ x −µ σ y +σ z +α∆T

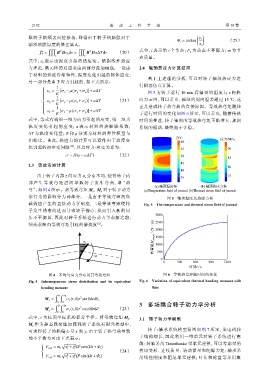
 图 5 为转子运行 10 min 后轴颈的温度与 z 向热

 E




 1 [ ] 应力云图，可以看出，轴颈的周向温差超过 15 ℃，这
 ε y = σ y −µ(σ z +σ x ) +α∆T （21）

 E

 正是造成转子热弯曲的直接原因。等效热弯矩随转


 1 [ ( )]
 ε z = σ z −µ σ x +σ y +α∆T


E 子运行时间的变化如图 6 所示，可以看出，随着传热
式中，等式右端第一项为应力引起的应变，第二项为 时间的推进，转子轴颈的等效热弯矩不断增大，加剧
温 度 变 化 引 起 的 应 变； α 表 示 材 料 的 热 膨 胀 系 数 ； 系统的振动，最终趋于平稳。
ΔT 为温度变化量；E 和 μ 分别为材料的弹性模量与
泊松比。由此，热应力的计算可以看作由于温度变 T/℃ 60 应力/MPa
化引起的初应变问题 [18] ，其总应力-应变关系为： 55 90
σ = D(ε−α∆T) （22）
50
85
2.3 等效弯矩计算 45 80
40
由于转子内部 z 向应力 σ z 分布不均，使得转子内 35 75
部 产 生 等 效 弯 矩 进 而 导 致 转 子 发 生 弯 曲， 即 “ 热
(a) 轴颈温度场 (b) 轴颈热应力场
弓”，如图 4 所示。热等效弯矩 M x 、M y 对于转子动力 (a)Temperature field of journal (b)Thermal stress field of journal

学行为的影响分为两部分，一是由于等效弯矩的负 图 5 轴颈温度及热应力场
载效应产生的直接动力学响应，二是等效弯矩使转 Fig. 5 The temperature and thermal stress field of journal
子发生热弯曲进而导致转子偏心，从而引入新的同
3000

步不平衡量，因此对转子系统进行动力学求解之前，
热弯矩M thermal / (N·m) 1500
须先求解由等效弯矩引起的静挠度 。 2500
[6]
2000
σ z 1000
M 500
0
0 300 600 900 1200
时间t / s

图 4 不均匀应力分布及其等效弯矩 图 6 等效热弯矩随时间的变化
Fig. 4 Inhomogeneous stress distribution and its equivalent Fig. 6 Variation of equivalent thermal bending moment with
bending moment time

w w 2π
R
2
M x = σ z (r,θ)r sinθdrdθ，
0 0
w w 2π 3 多 场 耦 合 转 子 动 力 学 分 析
R
2
M y = σ z (r,θ)r cosθdrdθ （23）
0 0
式中，r 为柱面坐标系的积分半径。将等效弯矩 M x 、 3.1 转子动力学模型
M y 作为静态载荷施加载到转子系统有限元模型中，
可求得转子的热偏心量 x 和 y，由于转子热弯曲导致 转子-轴承系统模型简图如图 7 所示，发电机转
的不平衡力可由下式表示： 子结构细长，因此利用一维单元对转子系统进行离
散：转轴采用 梁单元建模，可以考虑梁的
 √ Timoshenko
2
2
2
 x +y Ω cos(Ωt +Φ i )
 F nxi = m i
 i i
 （24） 剪切变形、连续质量、转动惯量和陀螺力矩；轴承采
 √

 2 2 2
 x +y Ω sin(Ωt +Φ i )
F nyi = m i 用线性刚度和阻尼单元建模；叶片和轮盘等采用集
i i