Page 129 - 《振动工程学报》2025年第9期

第 9 期 孙艳坤，等：飞机吊架集中质量-弯曲梁模型与振动特性分析 2059

、
P 0 传递矩阵 U 1 U 5 分别为：
y 0 = − sin(Ωt) （28）
m 0 Ω 2  
 1 0 0 0  

基于文献 [9] 实测发动机振动载荷谱数据，得到   0 1 0   


 0   （32）
U 1 =    

发动机在起飞、巡航和空慢三种工况下产生的振动  0 0 1 0   

  1  
u 0 0 1
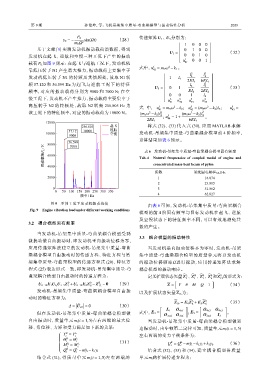
载荷 P 0 如图 9 所示：在起飞与巡航工况下，发动机依 41
式中， u = m 1 ω −k 1 。
2
1
靠低压转子 N1 产生最大推力，振动载荷主要集中于 41
 l 2 l 3 
发动机低压转子 N1 的转频及其倍频处，故取 N1 转   1 4 4  

 l 4  
 
  2EI 4 6EI 4  
频 57.120 和 56.599 Hz 为起飞与巡航工况下的特征    l 4 l 2   

U 5 =  0 1 4     （33）


频率，对应的振动载荷分别为 9000 和 7000 N；在空    EI 4 2EI 4   

 0 0 1 l 4    


慢工况下，发动机不产生推力，振动载荷主要集中于   5 5 5 5  
u 41 u 42 u 43 u 44
高压转子 N2 的转频处，故取 N2 转频 256.805 Hz 为
式 中， u = m 5 ω −k 2 ； u = (m 5 ω −k 2 )l 4 ； u =
5
5
2
5
2
43
42
41
该工况下的特征频率，对应的振动载荷为 10000 N。 (m ω −k 2 )l 2 4 (m 5 ω −k 2 )l 3 4
2
2
5
5
； u = 1+ 。
44

12000 2EI 4 6EI 4
256.805 起飞 将式 (32)、(33) 代入式 (30)，应用 MATLAB 求解
57.12 10000 巡航
10000 空慢 发动机-吊架集中质量-弯曲梁耦合模型前 4 阶频率，
9000
计算结果如表 6 所示。
56.599
8000
振动载荷P 0 / N 6000 Tab. 6 Natural frequencies of coupled model of engine and
7000
表 6 发动机-吊架集中质量-弯曲梁耦合模型固有频率
concentrated mass-bent beam of pylon
4000

阶数 系统固有频率 ω k /Hz
2000 1 16.074
2 23.815
0 3 51.862
0 50 100 150 200 250 300 350
4 62.827
频率 / Hz

图 9 不同工况下发动机振动载荷
由表 6 可知，发动机-吊架集中质量-弯曲梁耦合
Fig. 9 Engine vibration load under different working conditions
模型的前 4 阶固有频率与目标发动机在起飞、巡航
及空慢状态下的特征频率不同，可以有效地避免共
3.2 耦合模型固有频率
振的产生。

当发动机-吊架集中质量-弯曲梁耦合模型受到
3.3 耦合模型的振动特性
微扰动做自由振动时，即发动机垂向振动位移为零，
应用传递矩阵法建立的发动机-吊架集中质量-弯曲 当发动机垂向振动位移不为零时，发动机-吊架
梁耦合模型自由振动时的传递方程、特征方程与吊 集中质量-弯曲梁耦合模型的质量单元将以发动机
架集中质量-弯曲梁模型的传递方程式 (20)、特征方 的振动位移频率 Ω进行振动，应用传递矩阵法求解
程式 (25) 表达形式一致，即发动机-吊架集中质量-弯 耦合模型的振动响应。
曲梁耦合模型自由振动时的传递方程为： 定义扩展状态矢量 b L b R b 0 b 0 Z 的形式为：
Z 、
Z 、
Z 、
b 0
Z 和
i i 1 6 12
0
R
0
U 1−5 Z +U 6−12 E 2 Z − Z = 0 （29） [ ] （34）
Z =
U 6−12 E 1 U l 5 1 6 12 b Y θ M Q 1
发动机-吊架集中质量-弯曲梁耦合模型自由振 以及扩展状态矢量 Z I6 为：
b
动时的特征方程为：
b L
b 0
Z I6 = E 4 Z + E 5 Z （35）
b
6 6
∆ = ¯ = 0 （30） [ ] [ ]

U all
但在发动机-吊架集中质量-弯曲梁耦合模型做 式中， E 4 = I 4 O 4×1 ; E 5 = O 4×2 O 4×3 。
O 3×4 O 3×1 O 3×2 I 3
自由振动时，质量单元 m i (i = 1,5)左右两端的最大位 当发动机-吊架集中质量-弯曲梁耦合模型做强
移、角位移、力矩和受力满足如下新的关系： 迫振动时，由牛顿第二定律可知，质量单元 m i (i = 1,5)

R
 Y = Y L
 i i 左右两端的受力平衡条件为：


 Θ = Θ L
R

 i i （31） R L
 R L （36）
 M = M Q = Q −m¨y i −k 1 y i +k 1 y 0

i
i
 i i

 R L
 结合式 (32)、(33) 和 (34)，建立耦合模型各质量
Q = Q −m¨y i −k 1 y i
i i
结合式 (31)，得质量单元 m i (i = 1,5)左右两端的 单元 m i 的扩展传递方程为：