Page 10 - 《振动工程学报》2025年第9期

位移
−0.0
时间
缓冲器行程均值
位移
时间
缓冲器行程标准差
载荷
−1
时间
缓冲器行程
垂向轮胎力均值
−50
载荷
−100
−150 位移
位移
时间 对数坐标下 缓冲器行程
1940 振 动 工 程 学 报 第 38 卷
垂向轮胎力标准差

×10 5 ×10 −5
8 2.5
7
6 2.0
载荷 / N 5 4 3 PDF 1.5
2 1.0
1 0.5
0
−1 0
0 0.5 1.0 1.5 2.0 6.5 7.0 7.5 8.0 8.5 9.0 9.5 10.0
时间 / s 载荷 / N ×10 5
(e) 支柱轴向力均值
(c) 0.061 s垂向轮胎力PDF
(e) Mean of axial force on struts
(c) PDF of vertical tire force at 0.061 s
×10 4
2.0 10 0
1.8
1.6 −50
1.4 10
载荷 / N 1.0 PDF 10 −100
1.2
0.8
0.6
10 −150
0.4
0.2
0 6.5 7.0 7.5 8.0 8.5 9.0 9.5 10.0
0 0.5 1.0 1.5 2.0
载荷 / N ×10 5
时间 / s
(f) 支柱轴向力标准差 (d) 对数坐标下0.061 s垂向轮胎力PDF
(f) Standard deviation of axial force on struts (d) PDF of vertical tire force in logarithmic
coordinates at 0.061 s

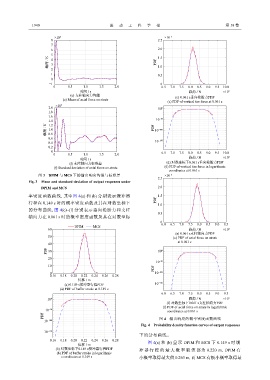
图 3 DPIM 与 MCS 下的输出响应均值与标准差 ×10 −5
2.5
Fig. 3 Mean and standard deviation of output responses under
DPIM and MCS 2.0
率密度函数曲线，其中图 4(a) 和 (b) 分别表示缓冲器 1.5
行程在 0.149 s 时的概率密度函数及其在对数坐标下 PDF 1.0
的分布曲线，图 4(c)~(f) 分别表示垂向轮胎力和支柱
0.5
轴向力在 0.061 s 时的概率密度函数及其在对数坐标
0
6.0 6.5 7.0 7.5 8.0 8.5 9.0 9.5
DPIM MCS
60 载荷 / N ×10 5
(e) 0.061 s支柱轴向力PDF
50 (e) PDF of axial force on struts
at 0.061 s
40
PDF 30 10 0
20
10 −50
10
PDF
0 10 −100
0.16 0.18 0.20 0.22 0.24 0.26 0.28
位移 / m
(a) 0.149 s缓冲器行程PDF 10 −150
(a) PDF of buffer stroke at 0.149 s
6.0 6.5 7.0 7.5 8.0 8.5 9.0 9.5
10 0 载荷 / N ×10 5
(f) 对数坐标下0.061 s支柱轴向力PDF
(f) PDF of axial force on struts in logarithmic
10 −50 coordinates at 0.061 s
PDF
10 −100 图 4 输出响应的概率密度函数曲线
Fig. 4 Probability density function curves of output responses
10 −150
下的分布曲线。
0.16 0.18 0.20 0.22 0.24 0.26 0.28 图 4(a) 和 (b) 显 示 DPIM 和 MCS 下 0.149 s 时 缓
位移 / m
(b) 对数坐标下0.149 s缓冲器行程PDF 冲 器 行 程 的 最 大 概 率 取 值 都为 0.220 m， DPIM 有
(b) PDF of buffer stroke in logarithmic
coordinates at 0.149 s 小概率取得最大值 0.263 m，而 MCS 有极小概率取得最

−5

载荷
垂向轮胎力

−50

−100

−150

载荷
对数坐标下 垂向轮胎力

−5

载荷
支柱轴向力

−50

−100

−150

载荷
对数坐标下 支柱轴向力