Page 226 - 《软件学报》2025年第5期

2126 软件学报 2025 年第 36 卷第 5 期

1.2 Base 250 600
λ A =e −1
λ A =e −2 200 Base 500 Base
λ A =5e −3
1.0
Supervised loss 0.8 λ A =5e −4 ALCW loss 150 λ A =e −2 Ratio 400 λ A =e −2
λ A =e −1
λ A =e −1
λ A =e −3
λ A =5e −3
λ A =5e −3
λ A =e −3
λ A =e −3
300
λ A =5e −4
λ A =5e −4
100
200
0.6
0.4 50 100
0 0
0 4 8 12 16 20 24 28 32 36 40 0 4 8 12 16 20 24 28 32 36 40 0 4 8 12 16 20 24 28 32 36 40
Epochs Epochs Epochs
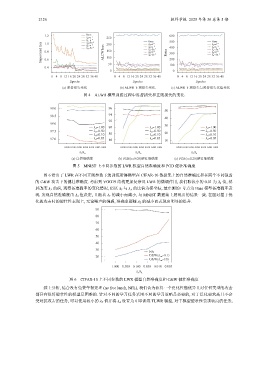
(a) 监督损失变化 (b) ALWR 正则损失变化 (c) ALWR 正则损失与监督损失比值变化
图 4 ALWR 模型训练过程中监督损失和正则损失的变化

99.0 96
50
94
98.5
40
92
99.0 30
λ A =1.00 90 λ A =1.00 λ A =1.00
97.5 λ A =0.50 λ A =0.50 λ A =0.50
λ A =0.10 88 λ A =0.10 20 λ A =0.10
97.0 λ A =0.05 86 λ A =0.05 10 λ A =0.05
0.200 0.100 0.050 0.020 0.010 0.005 0.001 0.200 0.100 0.050 0.020 0.010 0.005 0.001 0.200 0.100 0.050 0.020 0.010 0.005 0.001
λ T /λ A λ T /λ A λ T /λ A
(a) 自然准确率 (b) PGB(ϵ=0.05)健壮准确率 (c) PGB(ϵ=0.20)健壮准确率
图 5 MNIST 上不同参数的 LWR 模型自然准确度和 PGD 健壮准确度

图 6 给出了 LWR 在不同正则参数下的训练所得模型在 CIFAR-10 数据集上的自然准确度和在两个不同强弱
的 C&W 攻击下的健壮准确度. 考虑到 VGG19 结构更加复杂且 LWR 的微调作用, 我们取较小的 0.01 为 λ A 值, 然
λ A 的比值为横坐标, 最左侧的+号点为 Base 模型各准确率表
后改变 λ T 的值, 观察各准确率的变化情况, 仍以 λ T 与
现. 发现自然准确度由 λ A 值决定, 且随着 λ T 的减小而减小, 与 MNIST 数据集上展现出的结果一致. 在面对基于优
化的攻击时的健壮性表现上, 无论噪声的强弱, 准确率都随 λ T 的减小而表现出明显的提升.

90
80
70
60
50
40
30
NA
C&W(λ cw =0.1)
20
C&W(λ cw =10)
1.000 0.500 0.100 0.050 0.010 0.005
λ T /λ A
图 6 CIFAR-10 上不同参数的 LWR 模型自然准确度和 C&W 健壮准确度

综上分析, 结合没有免费午餐定理 (no free lunch, NFL), 我们认为获得一个泛化性能优异且对任何类型的攻击
都具有很好健壮性的模型是困难的. 针对不同的学习任务采用不同的学习策略是必要的, 对于泛化要求高且不会
受对抗攻击的任务, 可以使用较小的 λ T 值并将 λ A 设置为 0 即训练 TLWR 模型, 对于模型健壮性要求较高的任务,