Page 225 - 《软件学报》2025年第5期

王益民 等: 面向卷积神经网络泛化性和健壮性权衡的标签筛选方法 2125

epoch 后超过 Base 模型的相应损失, 且最终趋于平坦, 证明由公式 (21) 训练的模型增大了正确标签筛选的网络权
重参数的二范数值, 且正则项的添加导致模型的监督损失也在上升. 在深度学习中, 虽然更高的监督损失意味着更
低的自然准确度, 但在 TLWR 方法中, 优化正则损失, 即增大干净样本标签筛选的权重参数向量的二范数能够削
弱这一影响. 同时, 监督损失的变化关于正则项系数是敏感的, 调高系数很容易造成监督损失过高, 进而导致模型
无法收敛的问题, 虽然极小的系数能够起到训练效果, 但通过大量的调参实验来选择合适的系数会让训练任务变
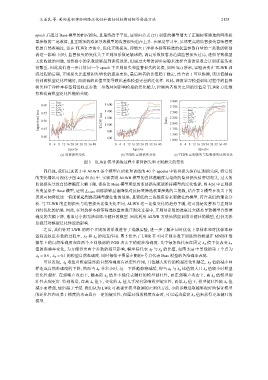
得繁重. 因此我们进一步计算同一个 epoch 下正则损失和监督损失的比值, 如图 3(c) 所示, 实验表明在 TLWR 训
练过程的后期, 正则损失比监督损失增长的速度更快, 最后两者的比值趋于稳定, 结合表 1 可以推测, 该比值越高
得到的模型泛化性越好, 而较低的比值可能导致比基准模型更差的泛化性. 因此, 深度学习模型训练过程中的监督
损失和干净样本标签筛选权重参数二范数共同影响模型的泛化能力, 控制两者损失之间的比值是 TLWR 方法维
持和提高模型泛化性能的关键.

3 000
Base Base
0.60 λ T =5e −7 1 600 λ T =5e −7
λ T =e −7 λ T =e −7 2 750
λ T =5e −8 1 400 λ T =5e −8 2 500 Base
Supervised loss 0.50 TLCW loss 1 200 Ratio 2 250 λ T =5e −8
λ T =e −8
λ T =e −8
λ T =5e −7
0.55
λ T =5e −9
λ T =5e −9
λ T =e −7
λ T =e −8
λ T =5e −9
2 000
1 000
0.45
1 750
800
1 500
0.40
600
1 000
0 4 8 12 16 20 24 28 32 36 40 0 4 8 12 16 20 24 28 32 36 40 0 4 8 12 16 20 24 28 32 36 40
Epochs Epochs Epochs
(a) 监督损失变化 (b) TLWR 正则损失变化 (c) TLWR 正则损失与监督损失比值变化
图 3 TLWR 模型训练过程中监督损失和正则损失的变化

同样地, 我们记录表 2 中 ALWR 各个模型在后处理训练的 40 个 epochs 中监督损失值和正则损失值, 将它们
的变化情况可视化于图 4(a) 和 (b) 中. 实验表明 ALWR 模型的自然准确度与最终的监督损失值密切相关, 过大的
监督损失导致自然准确度大幅下降, 保持比 Base 模型更低的监督损失更能维持模型的泛化性能. 图 4(b) 中正则损
失明显低于 Base 模型, 证明 L ALWR 训练能够显著降低对抗标签筛选权重参数的二范数, 结合表 2 模型在攻击下的
表现可知降低这一值能够起到提高模型健壮性的效果, 且更低的二范数值带来更健壮的模型, 符合我们的理论分
析. 与 TLWR 的正则损失与监督损失比值变化不同, ALWR 这一比值变化的趋势平缓, 这可能是监督项与正则项
同时优化的结果. 因此, 在对抗样本标签筛选权重参数正则化过程中, 正则项系数的选取过大极易导致模型自然准
确度的大幅下降, 选取过小则无法训练出健壮的模型. 因此利用 ALWR 方法虽然能训练出健壮的模型, 但仍无法
忽视其对模型泛化性能的影响.
之后, 我们针对 LWR 的两个正则项的系数进行了消融实验, 进一步了解在同时优化干净样本和对抗样本标
λ A 的相互作用. 图 5 给出了 LWR 在不同正则参数下训练所得模型在 MNIST 数
签筛选权重参数的过程中, λ T 和
据集上的自然准确度和在两个不同强弱的 PGD 攻击下的健壮准确度. 其中每条线代表在固定 λ A 值下仅改变 λ T
值的准确率变化, 为方便得出两个参数的相互影响, 横坐标代表 λ T 与 λ A 的比值, 如图 5(a) 中黑线的第 1 个点为
λ A = 0.5 λ T = 0.1 的模型自然准确度. 同时每张子图最左侧的+号点代表 Base 模型的各准确率表现.
,
可以发现, λ A 取值对模型最终的自然准确度有决定性作用, 且值越大所得的模型泛化性越差, λ T 值的减小同
λ A 值较小时模型
样造成自然准确度的下降, 然而当 λ T 非常小时, 这一下降趋势将减缓, 即当 λ T 与 λ A 比值较大且
泛化性最好. 在弱噪声攻击下, 越高的 λ A 值并不能代表越好的模型健壮性, 而在强噪声攻击下, 高 λ A 值模型健
壮性表现更好. 特别的是, 在高 λ A 值下, 变化的 λ T 值几乎没有影响模型健壮性, 而低 λ A 值下, 模型健壮性随 λ T 值
减小而增强, 最后趋于平缓. 我们认为 LWR 可被视作模型微调的正则化方法, 小的参数选取能够很好地保证模型

的泛化性和对基于梯度的攻击具有一定的健壮性, 但面对强的梯度攻击时, 可以适当提高 λ A 值来获得更加健壮的
模型.