Page 17 - 摩擦学学报2025年第4期

第 4 期 束坤, 等: 接触几何参数对硬质薄膜断裂和分层失效行为的影响及其解耦分析 505

表 1 仿真分析参数 0.02时，随着t/R的增大，薄膜承载阶段(Stage I)所对应
Table 1 Simulation parameters for the
的压入深度h/t范围逐渐增加[图4(a)]；而如图4(b)所
numerical analyses
示，当t/R较小时(t/R≤0.01)，膜基系统将迅速进入基
Parameters Symbols Units Specifications
体承载阶段(Stage III). 换言之，随着t/R的减小，薄膜
Film thickness t μm 2
Indenter tip radius R μm 10~400 对系统承载行为的影响逐渐减小，当t/R减小到一定程
Film elastic modulus E f GPa 200
度时，薄膜对系统的承载行为影响可忽略不计，这与
Film Poisson’s ratio ν f − 0.25
文献[21]的分析结果一致.
Substrate elastic modulus E s GPa 210
Substrate Poisson’s ratio ν s − 0.30 2.2 接触几何参数对薄膜主应力和断裂损伤失效
Substrate yield strength σ ys GPa 1
行为的影响
8
Interfacial stiffness K MPa/mm 5×10
硬质固体薄膜的断裂与其拉伸主应力集中密切
如图3所示. 随着压入深度h/t的增加，基体的塑性变形 相关，其裂纹的起始满足下式 [19,20,33] ：
区域逐渐扩展[图3(a~c)]，最大等效塑性变形也逐渐增 ß σ 1 +|σ 1 | ™
r = (1)
大[图3(d)]. 根据ε 沿径向[图3(e)]和深度方向[图3(f)] 2σ max
pmax
所处的位置，可将加载过程分为3个主要阶段：第1阶 式中，σ 和σ max 分别代表薄膜的第一主应力和拉伸断
1
段(Stage I)为薄膜承载阶段，此时的膜基界面主要由 裂强度. 当r=1时，硬质薄膜开始出现断裂. 由文献[17,32]
于薄膜-基体的弹性变形而处于平滑承载的状态，ε pmax 的研究结果可知，弹塑性基体上硬质薄膜的断裂主要
位于基体表面靠近加载中心轴处[图3(a, e, f)]；第2阶 发生在加载过程中. 接触几何参数t/R=0.04的膜基系
段(Stage II)为薄膜和基体共同承载阶段，ε pmax 位于靠 统加载过程中，σ 的分布及其最大值σ 1max 的演化过程
1
近界面的基体顶部，随着h/t的增加沿径向远离加载中 如图5所示. 薄膜拉伸主应力(σ /σ >0)主要位于2个区
1
ys
心[图3(b, e, f)]，即基体材料发生了沿径向的塑性流 域：接触区内的薄膜底部和接触区外沿的薄膜表面.
动. 此时薄膜下表面出现显著的弯曲(bending)变形， 而上述2个区域的应力集中分别是加载过程Stage II和
可将其简化为中间夹紧的受载平板；第3阶段(Stage III) Stage III中薄膜弯曲和拉伸引起的(图3)，容易导致薄
为基体承载阶段，ε pmax 沿径向向外移动的同时沿深度 膜底部的径向裂纹(radial cracks)以及薄膜表面的环形
方向深入基体内部[图3(c, e, f)]. 此时，薄膜上表面接 裂纹(ring cracks) [6,20] .
触外沿出现显著的弯曲拉伸(stretching)，整个系统的 随着压入深度h/t的增大，系统承载由Stage II转变
承载状态也由膜基共同承载逐渐转变为主要由基体 为Stage III，薄膜最大拉伸主应力σ 1max 也由薄膜底部
承载，此阶段可将薄膜视为铰接点在钢基体浅表层接 转移到薄膜表面的接触区外沿，薄膜潜在的断裂形式
触边缘的受载简支梁. 也随之由底部径向裂纹转变为表面环形裂纹. 因此，
加载过程中，接触几何参数t/R对基体最大等效塑 可将该位置转移点(transferring point)作为薄膜的断裂
性变形ε pmax 所处位置的影响如图4所示，图4中箭头为 行为转变临界点.
承载阶段的转变点. 由ε pmax 所在径向位置可知当t/R≥ 接触几何参数t/R对薄膜主应力分布及其演化行

2.0 1.2

(a) Xiao′s analysis [18] (b) Xiao′s analysis [18]
Present analysis Present analysis
1.0 0.8
Normal stress, σ n /σ ys −1.0 Tangential stress, σ t /σ ys 0.4
0.0

−2.0 0.0

−3.0 −0.4
0 1 2 3 4 0 1 2 3 4
Radial distance, r/a Radial distance, r/a
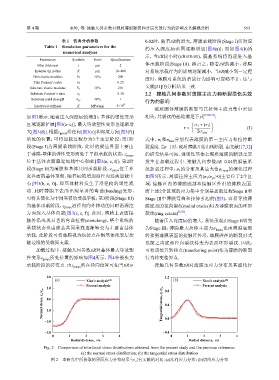
Fig. 2 Comparison of interfacial stress distributions obtained from the present study and the previous reference:
(a) the normal stress distribution; (b) the tangential stress distribution
图 2 本研究中所获取的界面应力分布结果与已有文献的对比：(a)法向应力分布；(b)切向应力分布