Page 33 - 《摩擦学学报》2021年第5期

622 摩 擦 学 学 报 第 41 卷

[17]
擦力随时间的变化保持不变，接触线长度、前进角和 触角保持常数，摩擦力进入稳定阶段. Gao等 对微液
后退角保持不变，前进角和后退角的差值为常数. 可 滴在硅基体表面的摩擦力变化趋势进行分析，获得了
以发现，固/液界面摩擦力首先要克服 “最大静摩擦 相似的结论. 硅的弹性模量为130~180 GPa [25] ，是典型
力”，然后固/液界面出现滑动，从而摩擦力稳定在1个 的硬基体，微液滴的表面张力在其表面引起的变形在
数值，表现为“动态摩擦力”. 对运动过程分析发现，当 皮米尺度，基体变形对固液界面摩擦力的影响可以忽
[26]
位移平台带动样品进行移动时，固液界面没有相对滑 略不计 . 对软基体表面而言，微液滴的表面张力会
动，微液滴下层随着位移平台运动. 由于液滴与悬臂 使软基体产生变形，从而改变固液界面摩擦性能. 微
梁之间毛细力的作用，液滴上层依然保持静止，因此 液滴在软基体表面引起的变形高度可以通过弹性毛
[27]
在液滴内部形成速度梯度. 根据牛顿定律，速度梯度 细长度，即表面张力与基体剪切模量的比值决定 .
会在液滴内部产生切应力，切应力大小与速度梯度和 微液滴表面张力引起的基体变形高度h*可通过公式(1)
[7]
液体的黏度呈正比 [22-24] . 悬臂梁在液体切应力的作用 进行计算 ：
下产生偏转，从而记录下切应力的大小，即最大静摩 γ lv sinθ
h = (1)
∗
擦力. 如图4所示，最大静摩擦力随着位移平台速度 G
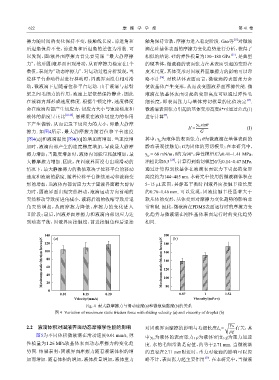
[图4(a)]和液滴黏度[图4(b)]的增加而增加. 当速度增 其中： γ 为液体的表面张力；θ为微液滴在基体表面的
lv
加时，液滴内部产生的速度梯度增加，导致最大静摩 静态表观接触角；G为固体的剪切模量；在本研究中，
擦力增加；当黏度增加时，液体内部能量耗散增加，最 γ = 68 mN/m；θ约为90°；弹性模量E为0.41~1.41 MPa，
lv
[28]
大静摩擦力增加. 因此，在固液界面没有出现滑动的 泊松比取0.5 ，计算得到剪切模量G为0.14~0.47 MPa.
情况下，最大静摩擦力的数值取决于位移平台的移动 通过计算得到软基体在液滴表面张力下引起的变形
速度和液滴的黏度. 随着位移平台继续运动和液滴变 高度约为144~485 nm. 本研究中使用的微液滴体积在
形的增加，当液体内部切应力大于固液界面最大剪切 5~15 μL范围，其静态平衡时固液界面接触半径长度
力时，固液界面出现突然滑动，液滴运动方向前端的 约0.76~1.46 mm. 可以发现，固液接触半径显著大于
突然移动导致前进角减小，液滴后端的收缩导致后退 软基体的变形，基体变形对摩擦力变化趋势的影响非
角突然增加，从而摩擦力降低，摩擦力的变化进入 常有限. 因此，微液滴在PDMS表面运行时的摩擦力变
Ⅱ阶段；最后，固液界面摩擦力和液滴内部切应力达 化趋势与微液滴在刚性基体表面运行时的变化趋势
到动态平衡，固液界面接触线、前进接触角和后退接 相同.

140 (a) 200 (b)
Maximum static friction force/μN 100 Maximum static friction force/μN 160
120
180
80
140
60
120
40
20
80
0 100
0.10 0.15 0.20 0.87 1 1.52
Velocity/(mm/s) Viscosity/(mPa·s)
Fig. 4 最大静摩擦力与滑动速度(a)和微液滴黏度(b)的关系
图 4 Variation of maximum static friction force with sliding velocity (a) and viscosity of droplet (b)

√
2.2 液滴体积对固液界面动态摩擦学性能的影响 对固液界面摩擦的影响与毛细长度 L c = γ lv 有关，其
ρg
图5为不同体积微液滴在滑动速度0.01 mm/s, 弹 中 γ lv 为液体的表面张力；ρ为液体密度；g为重力加速
性模量为1.26 MPa软基体表面动态摩擦力的变化趋 度. 水的毛细常数是定值，约等于2.71 mm. 当微液滴
势图. 结果表明：固液界面摩擦力随着液滴体积的增 的直径在2.71 mm附近时，重力对液滴的影响可以忽
[29]
加而增加. 随着体积的增加，液体质量增加，液体重力 略不计，表面张力起主要作用 . 在本研究中，当微液