Page 95 - 《爆炸与冲击》2025年第12期

第 45 卷 马路遥，等： 孔隙坍塌行为对多孔材料冲击压缩特性的影响理论分析 第 12 期

波波速并与试验值 [15-16] 进行了对比，如图 9 所 5 000
示。可以看出，简化孔隙坍塌模型计算得到的结 4 500
果与前驱冲击波波速的试验结果偏差过大。而 4 000 This method
采用本文中修正孔隙坍塌关系计算的前驱冲击 3 500 Simplified p-α model
波波速与试验值较为接近。 Precursor shock wave velocity/(m·s −1 ) 3 000
综上所述，本文中考虑材料孔隙坍塌行为 2 500
的计算模型能够较好地反映多孔材料的冲击波 2 000
1 500
结构，可以准确计算得到相关冲击波参数。 1 000
3.2 孔隙坍塌行为对冲击波参数的影响 Copper Copper Tungsten
(α 0 =1.475) (α 0 =1.205) (α 0 =1.521)
多孔材料的基体强度、初始孔隙度、剪切模
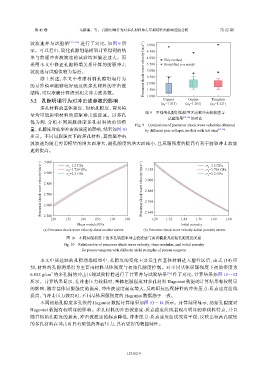
图 9 不同的孔隙坍塌模型下前驱冲击波波速与
量均可能影响材料的前驱冲击波波速。以多孔
试验结果 [15-16] 的对比
钨为例，分析不同屈服强度多孔材料的剪切模
Fig. 9 Comparison of precursor shock wave velocities obtained
量、孔隙度对前驱冲击波波速的影响，结果如图 10 by different pore collapse models with test ones [15-16]
所示。不同屈服强度下的多孔材料，其前驱冲击
波波速均随着剪切模量的增大而增大，随孔隙度的增大而减小，且屈服强度的提高有利于前驱冲击波波
速的提高。

3 000 σ y =1.2 GPa 3 120 σ y =1.2 GPa
Precursor shock wave velocity/(m·s −1 ) 2 800 Precursor shock wave velocity/(m·s −1 ) 3 000
σ y =1.729 GPa
σ y =1.729 GPa
2 900
σ y =2.2 GPa
σ y =2.2 GPa
2 880
2 700
2 760
2 600

2 500
120 132 144 156 168 180 2 640 1.20 1.32 1.44 1.56 1.68 1.80
Shear module/GPa Initial porosity
(a) Precursor shock wave velocity-shear module curves (b) Precursor shock wave velocity-initial porosity curves
图 10 不同屈服强度下的多孔钨前驱冲击波波速与剪切模量及初始孔隙度的关系
Fig. 10 Relationship of precursor shock wave velocity, shear modulus, and initial porosity
for porous tungsten with different yield strengths of porous tungsten

本文中所选取的孔隙坍塌模型中，孔隙度的变化主要发生在基体材料进入塑性区后，由式 (14) 可
知，材料的孔隙坍塌行为主要由材料基体强度与初始孔隙度控制。对不同基体屈服强度下初始密度为
6.052 g/cm 的多孔铜的冲击压缩试验特性进行了计算并与试验结果 [16] 作了对比，计算结果如图 11～12
3
所示。计算结果显示，在冲击压力较低时，基体屈服强度对多孔材料 Hugoniot 数据的计算结果有较明显
的影响，随着基体屈服强度的提高，冲击波速度起点增大，反映阻抗匹配特性的冲击压力-质点速度曲线
提高，当冲击压力较高时，不同基体屈服强度的 Hugoniot 数据趋于一致。
不同初始孔隙度多孔铁的 Hugoniot 数据计算结果如图 13～14 所示。计算结果显示，初始孔隙度对
Hugoniot 数据有较明显的影响。多孔材料的冲击波速度-质点速度曲线表现出明显的非线性特点，并且
随着初始孔隙度的提高，冲击波波速的起点降低，冲击压力-质点速度曲线变得平缓，反映出较高孔隙度
的多孔材料在冲击时具有更低的界面压力，具有更好的吸能特性。

123102-9