Page 97 - 《爆炸与冲击》2025年第9期

第 45 卷 崔 鹏，等： 动荷载下硅砂的破碎特性及吸能效应试验研究 第 9 期

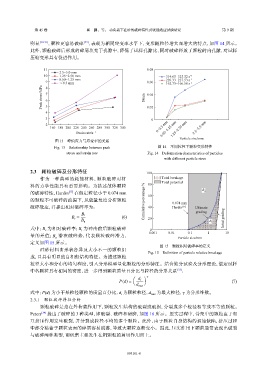
明显 [30-31] ，颗粒更容易破碎 [32] ，表现为相同应变率水平下，变形随粒径增大而增大的特点，如图 14 所示。
此外，颗粒破碎后形成的碎屑填充于孔隙中，降低了试样孔隙比，同时破碎释放了颗粒的内孔隙，对试样
压缩变形具有促进作用。

11 2.5−5.0 mm 0.08
10 1.25−2.50 mm 314.65−325.52 s −1
9 8 0.60−1.25 mm 0.06 220.33−227.53 s −1
＜0.3 mm
162.73−166.50 s
−1
Peak stress/MPa 7 6 Strain 0.04

4 5 0.02
3 0
0.60−1.25 mm
2
160 180 200 220 240 260 280 300 320 340 0−0.3 mm 1.25−2.50 mm 2.5−5.0 mm
Strain rate/s −1
图 13 峰值应力与应变率的关系 Particle size/mm
Fig. 13 Relationship between peak 图 14 不同粒径下颗粒变形特性
stress and strain rate Fig. 14 Deformation characteristics of particles
with different particle sizes

2.3 颗粒破碎及分形特征 100
作为一种典型的耗能材料，颗粒破碎对材 Total breakage
Total potential
料的力学性能具有重要影响。为描述散体颗粒 80
的破碎特性，Hardin [27] 在假定粒径小于 0.074 mm 60 B p
的颗粒不可破碎的前提下，从能量角度分析颗粒 Cumulative percentage/% 0.074 mm
破碎效应，并提出相对破碎率为： 40 Hardin [27] Ultimate
B t grading
B r = (6) 20 Intial grading
B p B t
式中：B 为相对破碎率；B 为冲击前后颗粒破碎 0
t
r
0.001 0.01 0.1 1 10
量的差值；B 潜在破碎势，代表颗粒破碎潜力，
p
Particle size/mm
定义如图 15 所示。
图 15 颗粒相对破碎率的定义
硅砂材料由形状各异及大小不一的颗粒组
Fig. 15 Definition of particle relative breakage
成，且具有明显的自相似结构特征。为描述颗粒
粒径大小和分布的均匀程度，引入分形模型量化颗粒的分形特征。结合筛分试验及分形理论，假定试样
中各颗粒具有相同的密度，进一步得到颗粒质量百分比与粒径的分形关系 [33] ：
Å ã γ
d i
P(d) = (7)
d max
式中：P(d) 为小于某粒径颗粒的质量百分比，d 为颗粒粒径，d x 为最大粒径，γ 为分形维数。
i
ma

2.3.1 颗粒破碎特征分析
颗粒破碎是指在外荷载作用下，颗粒发生结构的破裂或破损，分裂成多个粒径相等或不等的颗粒。
Peters [34] 提出了破碎的 3 种类型，即破裂、破碎和研磨，如图 16 所示。压实过程中，骨架中的颗粒由于相
互挤压作用发生破裂，并分裂成粒径不均的多个颗粒。此外，由于颗粒自身结构的初始缺陷，挤压过程
中部分粘着于颗粒表面的碎屑容易脱落，导致大颗粒逐渐变小。因此，压实作用下颗粒通常表现出破裂
与破碎两种类型，而研磨主要发生在粗颗粒的剪切作用面上。

093101-8