Page 99 - 《爆炸与冲击》2025年第9期

第 45 卷 崔 鹏，等： 动荷载下硅砂的破碎特性及吸能效应试验研究 第 9 期

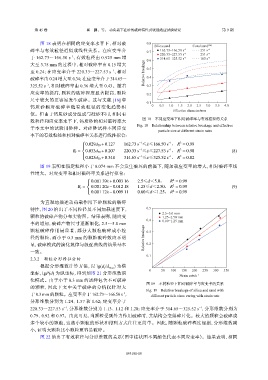
图 18 表明在相同的应变率水平下，相对破 0.8 Silica sand Coral sand [16]
碎率与有效粒径近似成线性关系。在应变率介 0.7 162.73−166.50 s −1 251 s −1
−1
−1
于 162.73～166.50 s ，有效粒径由 0.925 mm 增 0.6 220.33−227.53 s −1 251 s −1
−1
314.65−325.52 s
165 s
大至 3.75 mm 的过程中，相对破碎率由 0.15 增大
至 0.24；在应变率介于 220.33～227.53 s ，相对 Relative breakage 0.5
−1
破碎率由 0.24 增大至 0.34；在应变率介于 314.65～ 0.4
325.52 s ，相对破碎率由 0.36 增大至 0.43。随着 0.3
−1
应变率的提高，颗粒的破碎程度显著提高，颗粒 0.2
尺寸较大的更容易发生破碎。这与文献 [16] 中
0.1
钙 质 砂 相 对 破 碎 率 随 有 效 粒 径 的 变 化 趋 势 相 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
Effective diameter/mm
似。但由于钙质砂成分组成与硅砂不同，相同有
图 18 不同应变率下相对破碎率与有效粒径的关系
效粒径和应变率水平下，钙质砂的相对破碎率大
Fig. 18 Relationship between relative breakage and effective
于本文中的试验用砂样。对硅砂试样不同应变
particle size at different strain rates
率下的有效粒径和相对破碎率关系进行线性拟合：
 −1 −1 2
0.029d 50 +0.127 162.73 s ≤˙ε≤166.50 s ， R = 0.99

2
−1
−1
B r = 0.033d 50 +0.207 220.33 s ≤˙ε≤227.53 s ， R = 0.98 (8)

0.025d 50 +0.348 314.65 s ≤˙ε≤325.52 s ， R = 0.82
 −1 −1 2
图 19 表明在假定粒径小于 0.074 mm 不会发生破坏的前提下，随加载应变率的增大，相对破碎率线
性增大。对应变率和相对破碎率关系进行拟合：

2
 0.001 39˙ε+0.003 16 2.5≤d＜5.0， R = 0.99
2
B r = 0.001 20˙ε−0.012 18 1.25≤d＜2.50， R = 0.99 (9)
0.001 12˙ε−0.009 11 0.60≤d＜1.25， R = 0.99
 2
为直观地描述动荷载作用下砂颗粒的破碎
特性，图 20 给出了不同粒径及不同加载速度下， 0.5
2.5−5.0 mm
颗粒的破碎产物分布实物图。结果表明，随应变 1.25−2.50 mm
0.4 0.60−1.25 mm
率的增加，破碎产物尺寸逐渐细化，2.5～5.0 mm
颗粒破碎作用最显著，部分大颗粒破碎成小粒 0.3
径的颗粒，而小于 0.3 mm 的颗粒破碎效应不明 Relative breakage
显，破碎模式的演化规律与级配曲线的结果基本 0.2
一致。

0.1
2.3.2 颗粒分形特征分析
根据分形维数计算方法，以 lg(d /d max ) 为横
i
坐标，lgP(d) 为纵坐标，得到如图 21 分形维数演 0 50 100 150 200 250 300 350
Strain rate/s −1
化模式。由于小于 0.3 mm 的试样包含不可破碎
图 19 不同粒径下相对破碎率与应变率的关系
的颗粒，因此下文中关于破碎的分析仅针对大
Fig. 19 Relative breakage of silica and sand with
−1
于 0.3 mm 的颗粒。应变率介于 162.73～166.50 s ， different particle sizes varing with strain rate
分形维数分别为 1.24、1.57 和 1.62；应变率介于
−1
−1
220.33～227.53 s ，分形维数分别为 1.13、1.12 和 1.28；应变率介于 314.65～325.52 s ，分形维数分别为
0.79、0.92 和 0.97。由此可见，当颗粒受到外力作用破碎时，其结构会变得碎片化。较大的颗粒会破碎成
多个较小的颗粒，这些小颗粒的形状和排列方式往往更简单。因此，随颗粒破碎程度加剧，分形维数减
小，证明大颗粒比小颗粒更容易破碎。
图 22 给出了有效粒径与分形维数的关系（图中柱状图不同颜色代表不同应变率）。结果表明，相同

093101-10