Page 96 - 《爆炸与冲击》2025年第9期

第 45 卷 崔 鹏，等： 动荷载下硅砂的破碎特性及吸能效应试验研究 第 9 期

大；相同粒径下，应变率越高，峰值应力越大。观 6
C
察砂的应力-应变特征曲线，可将砂的变形分为 5 Plastic phase
弹性阶段（OA）、屈服阶段（AB）、塑性阶段（BC） B Unloading phase D
和卸荷阶段（CD），如图 11 所示。在弹性阶段，
应力与应变成线性关系，荷载主要由砂骨架承 Stress/MPa 4 3
担，且应力未超过骨架弹性极限；在屈服阶段，应 2 Yield phase
力快速升高，砂骨架及孔隙开始变形破坏，颗粒 1 A
发生滑移，细颗粒逐渐填充孔隙；在塑性阶段，颗 Elastic phase
O
粒破碎并发生重组，破碎的细颗粒逐渐填充孔 0 0.005 0.010 0.015 0.020 0.025 0.030 0.035
隙，试样被压得密实，颗粒之间难以滑动，应力达 Strain
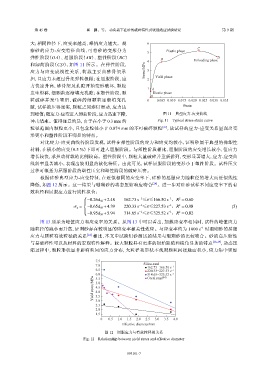
到峰值；随应力-应变进入卸荷阶段，应力迅速下降， 图 11 典型应力-应变曲线
冲击结束。值得注意的是，由于在小于 0.3 mm 的 Fig. 11 Typical stress-strain curve
粒径范围内颗粒更小，且包含粒径小于 0.074 mm 的不可破碎颗粒 [27] ，故试样的应力-应变关系呈现出变
形更小和塑性阶段不明显的特点。
对比应力-应变曲线各阶段发现，试样在弹性阶段的应力和应变均较小，证明砂属于典型的弹塑性
材料，在极小的应变（0.5 %）下即可进入屈服阶段。与塑性阶段相比，屈服阶段的应变增长较小，但应力
增长较快，承担动荷载的比例较高。塑性阶段中，颗粒大量破碎并重新排列，变形显著增大，应力-应变曲
线斜率显著减小，表现出较明显的软化特征。由此可见，试样屈服阶段的变形小于塑性阶段。试样压实
过程可概括为屈服阶段的塑性压实和塑性阶段的破碎压密。
根据硅砂典型应力-应变特征，在近似相同的应变率下，硅砂的屈服应力随粒径的增大而近似线性
降低，如图 12 所示。这一结果与珊瑚砂的动态压缩响应吻合 [24] 。进一步对硅砂试样不同应变率下的有
效粒径和屈服应力进行线性拟合：
 −1 −1 2
−0.26d 50 +2.48 162.73 s ≤˙ε≤166.50 s ，R = 0.60

−1
−1
2
σ y = −0.65d 50 +4.39 220.33 s ≤˙ε≤227.53 s ，R = 0.98 (5)

−0.95d 50 +5.94 314.65 s ≤˙ε≤325.52 s ，R = 0.82
 −1 −1 2
图 13 所示为峰值应力和应变率的关系。从图 13 中可以看出，加载应变率相同时，试样的峰值应力
随粒径的减小而升高，证明砂存在较明显的应变率相关性效应。与应变率约为 1 000 s 时珊瑚砂的屈服
−1
应力与颗粒有效粒径的关系 [24] 相比，本文中试验用砂测试的结果与珊瑚砂的比较吻合。砂的高压缩性
与易破碎性可以从材料的宏观特性解释。较大颗粒具有更多的初始缺陷和棱角显著的特点 [28-29] ，动态压
缩过程中，颗粒形状显著影响粒间的应力分布，大粒径和形状不规则颗粒间接触面积小，应力集中更加

7.5

7.0 Silica sand −1
162.73−166.50 s
6.5 220.33−227.53 s −1
6.0 314.65−325.52 s −1
Coral sand
5.5
[24]
Yield stress/MPa 5.0
4.5
4.0
3.5
3.0
2.5
2.0
1.5
0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
Effective diameter/mm
图 12 屈服应力与有效粒径的关系
Fig. 12 Relationship between yield stress and effective diameter

093101-7