Page 44 - 《爆炸与冲击》2025年第9期

第 45 卷 王 振，等： 平整壁面通道内冲击波传播试验研究 第 9 期

−1.2 m）、（5 m，0 m，−1.2 m）、（9 m，0 m，−1.2 m）、 Explosive
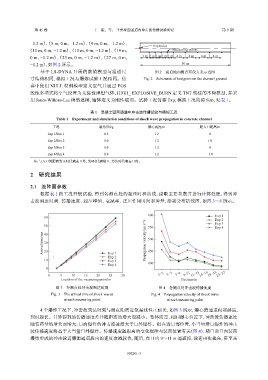
（11 m，0 m，−1.2 m）、（15 m，0 m，−1.2 m）、（19 m， Measuring points
0 m，−1.2 m）、（23 m，0 m，−1.2 m）、（27 m，0 m， 3 m 2 m 2 m2 m 2 m 4 m 4 m 4 m 4 m
−1.2 m），如图 2 所示。 30 m
基于 LS-DYNA 开展的数值模型与通道尺 图 2 通道地面测点布设方案示意图
寸结构相同，模拟工况与爆炸试验工况相同。仿 Fig. 2 Schematic of test point on the channel ground
真中使用 NULL 材料模型定义空气并通过 EOS
线性多项式将空气设置为无黏性理想气体，HIGH_ EXPLOSIVE_BURN 定义 TNT 药柱的本构模型，并采
用 Jones-Wilkins-Lee 模型建模，墙体定义为刚性壁面。试验工况简称 Exp，模拟工况简称 Sim，见表 1。

表 1 混凝土壁面通道中冲击波传播试验与模拟工况
Table 1 Experiment and simulation conditions of shock wave propagation in concrete channel
工况 装药量/kg 爆心高度/m 距入口距离/m
Exp 1/Sim 1 0.5 1.2 0
Exp 2/Sim 2 1.0 1.2 1.0
Exp 3/Sim 3 1.0 1.2 0
Exp 4/Sim 4 1.0 1.2 −1.0
注：与入口的距离为正时代表在口外，为0时代表堵口，为负时代表在口内。

2 研究结果

2.1 波阵面参数
根据表 1 的工况开展试验，得到各测点处的超压时程曲线，读取主要参数并进行计算处理，得到冲
击波到达时刻、传播速度、超压峰值、衰减率、正压作用时间和冲量，绘制分布折线图，如图 3～8 所示。

60 600 Exp 1
Exp 2
50 550 Exp 3
Exp 4
40
Arrival time/ms 30 Propagation velocity/(m·s −1 ) 500

450
20
Exp 2
10 Exp 1
Exp 3
Exp 4 400
0
0 5 10 15 20 25 30 3−5 5−7 7−9 9−11 11−15 15−19 19−23 23−27
Location of the measuring point/m Position/m
图 3 各测点处冲击波到达时刻 图 4 各测点处冲击波传播速度
Fig. 3 The arrival time of shock waves Fig. 4 Propagation velocity of shock wave
at each measuring point at each measuring point
4 个爆炸工况下，冲击波到达时刻与测点距离近似呈线性正相关，如图 3 所示，爆心离通道内部越远，
到时越长。计算得到的传播速度差异随距离的增大而减小。整体而言，相同爆心位置下，冲击波传播速度
随装药量的增大而增大；口内爆炸的冲击波速度大于口外爆炸。但在近口部位置，小当量堵口爆炸的冲击
波传播速度略高于大当量口外爆炸。传播速度随距离的变化规律与装药位置有关（图 4），堵口和口内装药
爆炸形成的冲击波近爆源通道段内的速度衰减较快，随后，在口内 9～11 m 通道段，波速再次提高，甚至高

092201-3