Page 85 - 《爆炸与冲击》2025年第5期

第 45 卷 左 庭，等： 冲击荷载下含铜矿岩能量耗散的数值模拟 第 5 期

纹的萌生、发育和扩展 [31-33] 。由于自适应有限离散元方法无需内聚单元模拟连续体变形过程，因此可以
提高计算精度。与传统 FDEM 相比，自适应有限离散元方法可大大缩短计算时间，有效降低计算成本 [34-37] 。

Triangular
Continuum elements
Joint
elements

(a) Continuum characterization in FDEM

Tensile T T Mode Ⅱ
f e Mode Ⅰ f e f e Mode Ⅰ-Ⅱ
Normal bond O s f e G Broken

G
Broken G Broken Mode Ⅰ
O O ρ O ρ Strain O O ρ Strain O O ρ O ρ Strain
Normal open Normal open Normal open
Model Ⅰ Model Ⅱ Model Ⅰ-Ⅱ
(b) Fracture constitutive model of the joint element

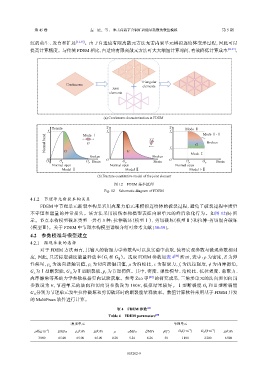
图 12 FDEM 基本原理
Fig. 12 Schematic diagram of FDEM
4.1.2 节理单元断裂本构关系

FDEM 中节理单元断裂本构是采用内聚力单元来模拟连续体的破裂过程，避免了破裂过程中质量
不守恒和能量的异常损失。该方法采用损伤本构模型表征内聚单元的峰后软化行为。如图 12(b) 所
示。节点本构模型破坏类型一共有 3 种：拉伸破坏（模型Ⅰ）、剪切破坏（模型Ⅱ）和拉伸-剪切混合破坏
（模型Ⅲ）。关于 FDEM 中节理本构模型详细介绍可参考文献 [38-39]。

4.2 参数校准与模型建立

4.2.1 微观参数的选择
对于 FDEM 方法而言，其输入的物理力学参数均可以从实验中获取，使得宏观参数与微观参数相对
应，因此，只需标定裂纹能量释放率（G 和 I G ）。选取 FDEM 参数如表 4 [40] 所示，表中：ρ 为密度，E 为弹
Ⅱ
n
性模量，p 为法向接触罚值，p 为切向接触罚值，μ 为泊松比，c 为黏聚力，f 为抗拉强度，ϕ 为内摩擦角，
t
t
G 为Ⅰ型断裂能，G 为Ⅱ型断裂能，p 为节理罚值。其中，密度、弹性模量、泊松比、抗拉强度、黏聚力、
f
I
Ⅱ
内摩擦角等基础力学参数根据室内试验获取。参考 Zuo 等 [40] 的研究成果，三角形单元的法向和切向罚
参数设为 E，节理单元的法向和切向罚参数设为 100E，模拟结果较好。Ⅰ型断裂能 G 和Ⅱ型断裂能
I
G 分别为节理单元发生拉伸破坏和剪切破坏时的断裂能量释放率。数值计算软件采用基于 FDEM 开发
Ⅱ
的 MultiFracs 软件进行计算。
[40]
表 4 FDEM 参数
Table 4 FDEM parameters [40]
三角形单元 节理单元
−2
−2
−3
ρ/(kg·m ) E/GPa p n /GPa p t /GPa μ c/MPa f t /MPa ϕ/(°) G I /(J·m ) G II /(J·m ) p f /GPa
3 080 65.00 65.00 65.00 0.28 5.26 8.26 30 1 100 2 200 6 500

053202-9