Page 80 - 《爆炸与冲击》2025年第5期

第 45 卷 左 庭，等： 冲击荷载下含铜矿岩能量耗散的数值模拟 第 5 期
w t
2
ε (t)dt (4)
W i = A s c e E 0 i
0
w t
2
ε (t)dt (5)
W r = A s c e E 0 r
0
w t
2
ε (t)dt (6)
W t = A s c e E 0 t
0
(7)
W d = W i −W r −W t
E 0 为弹性杆的弹性模量。
、
、
式中： ε i (t) ε r (t) ε t (t) 分别为入射、反射及透射波的应变，

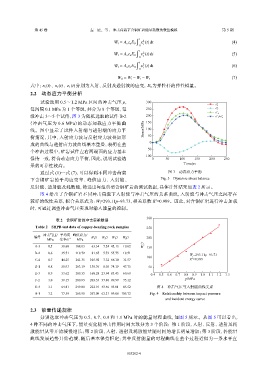
2.2 动态应力平衡分析
试验选用 0.5～1.2 MPa 区间的冲击气压 p， 300
σ i
每间隔 0.1 MPa 为 1 个等级，共分为 8 个等级，每 250 σ r
σ t
级冲击 3～5 个试件，图 3 为随机选取的试件 B-2 200 σ i +σ r
（冲击气压为 0.6 MPa）的动态加载应力平衡曲 150
线。图中显示了试件入射端与透射端的应力平 Stress/MPa 100
衡情况，其中，入射应力波与反射应力波叠加形 50
0
成的曲线与透射应力波曲线基本重叠，表明在整
−50
个冲击过程中，矿岩试件左右两端面的应力基本
−100
保持一致，符合动态应力平衡，因此，说明试验结 0 50 100 150 200 250
Time/μs
果的可靠性较高。
通过式 (1)～式 (7)，可以得到不同冲击荷载 图 3 动态应力平衡
下含铜矿岩的平均应变率、峰值应力、入射能、 Fig. 3 Dynamic stress balance
反射能、透射能及耗散能，筛选出每组典型含铜矿岩的测试数据，具体计算结果如表 2 所示。
图 4 给出了含铜矿岩不同冲击荷载下入射能与冲击气压的关系曲线，入射能与冲击气压之间存在
较好的线性关系，拟合关系式为：W =293.11p–93.73，相关系数 R =0.989。因此，对含铜矿岩进行冲击加载
2
i
时，可通过调整冲击气压实现对输入能量的控制。

300
表 2 含铜矿岩的冲击实验数据
Table 2 SHPB test data of copper-bearing rock samples 250
冲击气压/ 平均应 峰值应力/
编号 W i /J W r /J W t /J W d /J 200
MPa 变率/s −1 MPa
W i /J
A-3 0.5 30.68 108.03 63.34 7.24 45.13 10.62 150
B-2 0.6 35.71 119.72 81.67 5.73 55.75 19.51 W i =293.11p−93.73
100 2
C-4 0.7 44.25 141.35 105.92 7.32 66.10 31.57 R =0.989
D-1 0.8 50.93 163.19 130.76 8.05 74.19 47.75 50
E-3 0.9 53.62 189.55 168.28 23.94 83.45 60.60
0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3
p/MPa
F-2 1.0 59.15 200.93 203.33 37.88 89.99 75.12
G-4 1.1 64.81 249.80 222.91 43.46 93.01 85.52 图 4 冲击气压与入射能曲线关系
H-1 1.2 77.39 265.90 267.09 62.21 99.06 105.72 Fig. 4 Relationship between impact pressure
and incident energy curve

2.3 能量传递规律
分别选取冲击气压为 0.5、0.7、0.9 和 1.1 MPa 时的能量时程曲线，如图 5 所示。从图 5 可以看出，
4 种不同的冲击气压下，能量变化随冲击作用时间大致分为 3 个阶段： 第 1 阶段，入射、反射、透射及耗
散能量从零开始缓慢增长；第 2 阶段，入射、透射及耗散能量随时间的增长明显增加；第 3 阶段，各能量
曲线发展趋势开始趋缓，随后基本保持恒定；其中反射能量的时程曲线在整个过程近似为一条水平直

053202-4