Page 84 - 《爆炸与冲击》2025年第5期

第 45 卷 左 庭，等： 冲击荷载下含铜矿岩能量耗散的数值模拟 第 5 期

D b 为
式中： M (x) 为粒径小于 x 的碎块累积质量， M T 为碎块总质量， x 为碎块的粒径， x m 为碎块最大粒径，
矿岩碎块分布分形维数。
对式 (9) 左右两端同时去对数，化简可得：
M (x) x
lgy = lg = (3− D b )lg (10)
M T x m
根据式 (10) 可知，利用 lg[M(r)/M T ] lgr 拟合直线中的斜率可求得冲击荷载下含铜矿岩破碎块度的
-
分形维数。
图 10 给出了含铜矿岩破碎块度分形维数计算的双对数关系曲线，由图 10 可以看出，拟合曲线的线
性相关系数 R 均在 0.9 以上，说明在冲击荷载下岩石破碎块度的分布遵循统计意义上的自相似性。当
2
矿岩试件受到高速冲击荷载后，其内部的微缺陷开始延伸、扩展，最终导致试件发生宏观破坏，通常利用
碎块的分形表征岩石在冲击荷载下破碎的形成过程 [23-24] 。基于矿岩碎块的分形特点，可根据不同等级的
碎矿要求，选择适当的冲击能量，使矿岩碎块分布范围更均匀，以期达到最佳的破碎效果。
lg[M(r)/M T ] lgr 关系曲线，得出含铜矿岩的块度分形维数，绘制出含铜矿岩在单轴冲击
根据典型的 -
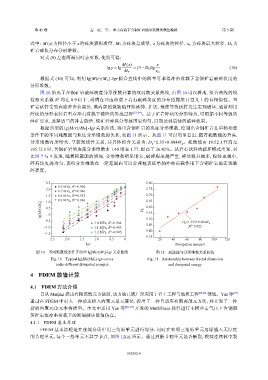
条件下的不同耗散能与块度分形维数的关系，如图 11 所示。从图 11 可以明显看出，随着耗散能的升高，
分形维数有所增大，呈较强线性关系，其具体拟合关系为：D =1.35+0.004W 。耗散能由 19.52 J 升高至
b d
105.72 J 时，含铜矿岩的块度分形维数由 1.40 增至 1.77，提高了 26.42%。从岩石试件的破坏模式出发，对
比图 7 与 9 发现，随着耗散能的增加，分形维数明显增大，破碎程度越严重，碎块数目越多，粒径也越小，
碎石块度越均匀，表明分形维数在一定范围内可以合理地表征单轴冲击荷载作用下含铜矿岩的宏观破
碎程度。

2.5 2 1.80
2.0 0.6 MPa, R =0.904 1.75
2
0.7 MPa, R =0.940
1.5 0.8 MPa, R =0.922 1.70
2
0.9 MPa, R =0.986
2
1.0
1.65
lg[M(r)/M T ] 0.5 0 D b 1.60
1.55
−0.5 1.0 MPa, R =0.984 1.50 D b =1.355+0.004W d
2
2
−1.0 1.1 MPa, R =0.983 1.45 R =0.925
2
2
−1.5 1.2 MPa, R =0.985 1.40
−2.5 −2.0 −1.5 −1.0 −0.5 0 1.35 20 40 60 80 100 120
lgr Dissipation energy/J
图 10 不同耗散能条件下典型 lg[M(r)/M T ]-lgr 关系曲线 图 11 耗散能与分形维数关系曲线
Fig. 10 Typical lg[M(r)/M T ]-lgr curves Fig. 11 Relationship between fractal dimension
under different dissipated energies and dissipated energy
4 FDEM 数值计算

4.1 FDEM 方法介绍
自从 Munjiza 提出有限离散元方法后，该方法已被广泛应用于岩土工程与地质工程 [25-26] 领域。Yan 等 [27]
通过在 FDEM 中引入一种动态插入内聚元单元算法，提出了一种自适应有限离散元方法，并开发了一种
新的内聚元单元本构模型。本文中运用 Yan 等 [28-30] 开发的 MultiFracs 软件进行不同冲击气压下含铜凝
灰矿岩在冲击荷载下的断裂破坏数值仿真。

4.1.1 FDEM 基本原理
FDEM 基本原理是在连续介质中用三角形单元进行划分，同时在相邻三角形单元边缘插入无厚度
的节理单元，每个三角单元不共享节点，如图 12(a) 所示。通过判断节理单元是否断裂，模拟连续体中裂

053202-8