Page 23 - 《爆炸与冲击》2023年第2期
P. 23
第 43 卷 李 瑞,等: 低温和低压环境下炸药爆炸冲击波的传播特性 第 2 期
和 UFC 3-340-02 规范 [20] 的对比结果如图 3 所示。从图 3 可以看出,这些经验公式的适用范围和计算结
果互有差异,这是由于早期的测试条件落后,仪器精度不够等多种原因导致的。
10 6 10 4
Henrych [12] Henrych [12] Kinney-Graham [17]
Brode [13] Held [14] Izadifard-Foroutan [7]
10 5 Held [14] Sadovkiy [15] Kingery-Bulmash [19]
Sadovkiy [15] UFC 3-340-02 [20]
Bajic [16] [17] 10 3 Numerical data
10
4
Δp m /kPa 10 3 Mills [18] (i/W 1/3 )/(Pa·s·kg −1/3 )
Kinney-Grahm
10 2 Izadifard-Foroutan [7] 10 2
UFC 3-340-02 [20]
(a) Numerical data (b)
10 1 10 1
10 −1 10 0 10 1 10 −1 10 0 10 1
Z/(m·kg −1/3 ) Z/(m·kg −1/3 )
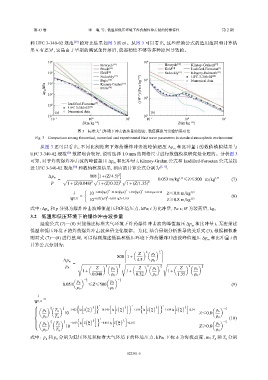
图 3 标准大气环境下冲击波参量的理论、数值模拟与实验结果对比
Fig. 3 Comparison among theoretical, numerical and experimental blast wave parameters in standard atmospheric environment
从图 3 还可以看出,不同比例距离下炸药爆炸冲击波峰值超压 Δp 和比冲量 i 的数值模拟结果与
m
UFC 3-340-02 规范 [20] 数据吻合较好,说明选择 1.0 mm 的网格尺寸进行数值模拟研究是合理的。分析图 3
可知,对于炸药爆炸冲击波的峰值超压 Δp 和比冲量 i,Kinney-Grahm 公式和 Izadifard-Foroutan 公式最接
m
近 UFC 3-340-02 规范 [20] 和数值模拟结果,相应的计算公式分别为 [7, 17] :
[ 2 ]
808 1+(Z/4.5)
∆p m 1/3 1/3
= √ √ √ 0.053 m/kg ≤Z≤500 m/kg (7)
p 1+(Z/0.048) 2 1+(Z/0.32) 2 1+(Z/1.35) 2
® 4 3 2
i 10 −3.423( lgZ) −10.143( lgZ) −7.558( lgZ) −1.614 lgZ+2.14 Z<0.8 m/kg 1/3
= 2 (8)
W 1/3 10 −0.07( lgZ) −0.853 lgZ+2.153 Z≥0.8 m/kg 1/3
式中:Δp 和 p 分别为爆炸冲击波峰值超压和环境压力,kPa;i 为比冲量,Pa·s;W 为装药量,kg。
m
3.2 低温和低压环境下的爆炸冲击波参量
经验公式 (7)~(8) 只能描述标准大气环境下炸药爆炸冲击波的峰值超压 Δp 和比冲量 i,无法描述
m
低温和低压环境下的炸药爆炸冲击波参量变化规律。为此,结合量纲分析推导的关系式 (3),根据相似准
则对式 (7)~(8) 进行整理,可以得到描述低温和低压环境下炸药爆炸冲击波峰值超压 Δp 和比冲量 i 的
m
计算公式分别为:
ñ
Å ã 2 Å ã 2 ô
Z p h 3
808 1+
4.5
∆p m p 0
=
Å ã 2 Å ã 2 Å ã 2 Å ã 2 Å ã 2 Å ã 2
p h Z p h 3 Z p h 3 Z p h 3
1+ 1+ 1+
0.048 p 0 0.32 p 0 1.35 p 0
1 1
Å ã − Å ã −
3 3
p h p h
0.053 ≤Z≤500 (9)
p 0 p 0
i
=
W 1/3
{ [ ( ) 1 ]} 4 { [ ( ) 1 ]} 3 { [ ( ) 1 ]} 2 [ ( ) 1 ]
Å ã 2Å ã 1 p h 3 p h 3 p h 3 p h 3 Å ã − 1
3 2 −3.423 lg Z −10.143 lg Z −7.558 lg Z −1.614 lg Z +2.14 3
p h T 0 p 0 p 0 p 0 p 0 p h
10 Z<0.8
p 0 T h p 0
{ [ ]} 2 [ ] (10)
Å ã 2 Å ã 1 ( ) 1 ( ) 1 Å ã − 1
p h 3 p h 3
3 2 −0.07 lg Z −0.853 lg Z +2.153 3
p h T 0 p 0 p 0 p h
10 Z≥0.8
p 0 T h p 0
式中: p 和 h p 分别为低压环境和标准大气环境下的环境压力,kPa;下标 h 为海拔高度,m;T 和 h T 分别
0
0
022301-5