Page 25 - 《爆炸与冲击》2023年第2期

第 43 卷 李 瑞，等： 低温和低压环境下炸药爆炸冲击波的传播特性 第 2 期

3.3 高海拔环境下的爆炸冲击波参量
高海拔环境是典型的低温和低压耦合大气环境，高海拔环境下环境温度和大气压力与海拔高度分
别有如下关系 [7, 22] ：
Å ã 5.255 88
h
T h = 288.15−0.006 5h，p h = 101.325 1− 0≤h≤11 000 m (11)
44 330
根据关系式 (11) 和空气状态方程 pM =ρRT，计算获得不同海拔高度 h 下的环境温度 T 、环境压力
h
r
p 和空气密度 ρ ，如表 3 所示。
h
h
将表 3 中不同海拔高度下的环境温度 T 和
h
表 3 不同海拔高度下的大气参数
环境压力 p 代入式 (5)～(6)，计算获得不同海拔
h
Table 3 Atmospheric parameters at different altitudes
高度下的空气状态参数，再利用 AUTODYN 有
−3
h/m T h /K p h /kPa ρ h /(kg∙m )
限元软件对不同海拔高度下炸药爆炸冲击波的
0 288.15 101.325 1.225
传播过程进行数值模拟研究。同时，将表 3 中不
4 500 258.90 57.728 0.777
同海拔高度下的大气参数代入式 (9)～(10)，计算
9 000 229.65 30.742 0.466
获 得 不 同 海 拔 高 度 下 的 爆 炸 冲 击 波 峰 值 超 压
Δp 和比冲量 i。相应爆炸冲击波参量的理论计算、数值模拟与实验数据对比结果，以及冲击波超压
m
Δp 和比冲量 i 随海拔高度 h 增加的变化率如图 6 所示。
m

10 5 100 10 3 100
Fitted curve (Eq.(9)), h=0 m (a) (b)
Fitted curve (Eq.(9)), h=4 500 m 50
10 4 Fitted curve (Eq.(9)), h=9 000 m 80 Fitted curve (Eq.(10)), h=0 m 0
Fitted curve (Eq.(10)), h=4 500 m
60 Fitted curve (Eq.(10)), h=9 000 m −50
10
3
Δp m /kPa 10 2 40 [(Δp m0 −Δp m9 000 )/Δp m0 ]/% (i/W 1/3 )/(Pa·s·kg −1/3 ) 10 2 −100 [(i 0 −i 9 000 )/i 0 ]/%
Numerical data, h=0 m
Numerical data, h=4 500 m 20 Numerical data, h=0 m −150
−200
10 1 Numerical data, h=9 000 m Numerical data, h=4 500 m
Experimental data, h=4 500 m [23] 0 Numerical data, h=9 000 m −250
(i 0 −i 9 000 )/i 0
(Δp m0 −Δp m9 000 )/Δp m0
10 0 −20 10 1 −300
10 −1 10 0 10 1 10 −1 10 0 10 1
Z/(m·kg −1/3 ) Z/(m·kg −1/3 )
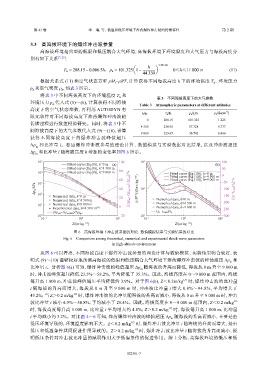
图 6 高海拔环境下冲击波参量的理论、数值模拟结果与实验结果的对比
Fig. 6 Comparison among theoretical, numerical and experimental shock wave parameters
in high-altitude environment
从图 6 可以看出，不同海拔高度下爆炸冲击波参量的理论计算与数值模拟、实验结果吻合较好，表
明式 (9)～(10) 能够较好地预测高海拔的低温和低压耦合大气环境下炸药爆炸冲击波的峰值超压 Δp 和
m
比冲量 i。分析图 6(a) 可知，爆炸冲击波的峰值超压 Δp 随海拔的升高而降低，海拔从 0 m 升至 9 000 m
m
时，冲击波峰值超压降低 23.5%～58.2%，平均降低了 35.3%。因此，海拔高度在 0～9 000 m 范围内，海拔
每升高 1 000 m，冲击波峰值超压平均降低约 3.9%。对于图 6(b)，Z＜0.2m/kg 1/3 时，爆炸冲击波的比冲量
i 随海拔的升高而增大，海拔从 0 m 升至 9 000 m 时，冲击波比冲量 i 增大 0.8%～94.8%，平均增大了
43.2%；当 Z＞0.2 m/kg 1/3 时，爆炸冲击波的比冲量随海拔的升高而减小，海拔从 0 m 升至 9 000 m 时，冲击
波比冲量 i 减小 4.9%～58.8%，平均减小了 28.4%。因此，海拔高度在 0～9 000 m 范围内，Z＜0.2 m/kg 1/3
时，海拔高度每升高 1 000 m，比冲量 i 平均增大约 4.8%；Z＞0.2 m/kg 1/3 时，海拔每升高 1 000 m，比冲量
i 平均减小约 3.2%。对比图 4～6 可知，炸药爆炸冲击波的峰值超压 Δp 随海拔的升高而减小，主要是由
m
低压环境导致的，环境温度影响不大。Z＜0.2 m/kg 1/3 时，爆炸冲击波比冲量 i 随海拔的升高而增大，是由
低压和低温条件共同促进作用导致的。Z＞0.2 m/kg 1/3 时，爆炸冲击波比冲量 i 随海拔的升高而减小，说
明低压条件对冲击波比冲量的减弱作用大于低温条件的促进作用。综上分析，高海拔环境的低压和低

022301-7