Page 21 - 《爆炸与冲击》2023年第2期

第 43 卷 李 瑞，等： 低温和低压环境下炸药爆炸冲击波的传播特性 第 2 期

表 1 爆炸冲击波传播问题中物理量的量纲幂次 表 2 爆炸冲击波传播问题中物理量的量纲幂次（初等变换）
Table 1 Dimensional power coefficients of physical Table 2 Dimensional power coefficients of physical quantities
quantities in the problem of in the problem of blast wave propagation
blast wave propagation (elementary transformation)
基本量纲 E p ρ r Δp m i t 参考物理量 E p ρ r Δp m i t
M 1 1 1 0 1 1 0 E 1 0 0 1/3 0 1/3 1/3
L 2 −1 −3 1 −1 −1 0 p 0 1 0 −1/3 1 1/6 −5/6
T −2 −2 0 0 −2 −1 1 ρ 0 0 1 0 0 1/2 1/2

[8]
根据 Π 定理 ，由表 2 可以得出爆炸冲击波参量峰值超压 Δp 、比冲量 i 以及冲击波到达时间 t 的无
m
量纲表达式：
 ( r )
∆p m 1/ 3
 p
 = f 1 1/ 3
 p E



i r p 1/ 3
 ( )
 E 1/ 3 p ρ = f 2 E 1/ 3 (2)
1/ 6 1/ 2


 tp 5/ 6 ( r )

 1/ 3
 = f 3 p
E ρ E 1/ 3
1/ 3 1/ 2
对于空气，有状态方程 pM =ρRT，式中 R 为理想气体常数，T 为环境温度，M 为空气相对分子质量；
r
r
相同炸药爆炸释放的总能量 E 主要取决装药质量 W。因此，式 (2) 可以转化为：

∆p m ( 1/ 3 )
 = f 1 Zp

 p



 1/ 2
T i ( )
= f 2 Zp 1/ 3 (3)
 W 1/ 3 p 2/ 3


 1/ 2 1/ 3
 T p t ( )

 = f 3 Zp 1/ 3
W 1/ 3
1/3
式中：Z 为比例距离，Z=r/W 。
从式 (3) 可以看出，炸药爆炸冲击波的比冲量 i 和冲击波到达时间 t 取决于环境温度 T 和环境压力
p 的影响，而爆炸冲击波峰值超压 Δp 则主要取决于环境压力 p 的影响。
m
2 爆炸冲击波参量的数值模拟
2.1 计算模型
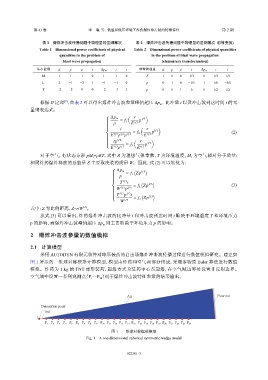
采用 AUTODYN 有限元软件对球形装药的自由场爆炸冲击波传播过程进行数值模拟研究。建立如
图 1 所示的一维球对称楔形计算模型，模型由炸药和空气两部分组成，采用多物质 Euler 算法进行数值
模拟。炸药为 1 kg 的 TNT 球形装药，起爆方式为装药中心点起爆，在空气域边界处设置非反射边界。
空气域中设置一系列观测点（P ～P ）用于爆炸冲击波特征参量的结果输出。
1
24

Air Flow out
Detonation point
TNT
P 1 P 2 P 3 P 4 P 5 P 6 P 7 P 8 P 9 P 10 P 11 P 12 P 13 P 14 P 15 P 16 P 17 P 18 P 19 P 20 P 21 P 22 P 23 P 24
图 1 一维球对称楔形模型
Fig. 1 A one-dimensional spherical symmetric wedge model

022301-3