Page 90 - 《软件学报》2020年第12期

3756 Journal of Software 软件学报 Vol.31, No.12, December 2020

• 非参数方法对总体的分布不做任何假设,直接或间接按照给定数据进行训练.常见的非参数方法包括
神经网络(反向传播网络 [27] 、循环神经网络 [30] 、长短期记忆网络 [31] 和状态空间网络 [32] )、支持向量回
[9]
归 [33,34] 、最近邻 [28] 和集成学习方法 等.

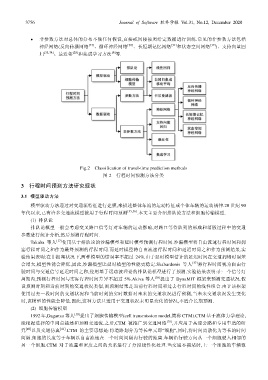
Fig.2 Classification of travel-time prediction methods
图 2 行程时间预测方法分类
3 行程时间预测方法研究现状

3.1 模型驱动方法
模型驱动方法通过对交通流特征进行建模,来描述整体车流的运动特征或个体车辆的运动规律.20 世纪 90
年代以来,已有许多交通流模型被用于行程时间预测 [35,36] .本文主要介绍排队论方法和细胞传输模型.
(1) 排队论
排队论模型一般会考虑交叉路口信号灯对车辆的运动影响,对路口等待队列的形成和消散过程中的交通
参数进行统计分析,然后预测行程时间.
Takaba 等人 [17] 使用基于排队论的沙漏模型和延时模型预测行程时间.沙漏模型将自由流速行程时间和拥
塞行程时间之和作为最终预测的行程时间.而延时模型将自由流速行程时间和延迟时间之和作为预测结果.实
验结果表明:在非拥塞状况下,两种模型的错误率不超过 24%.由于延时模型估计的延迟时间在交通拥堵时误差
会增大,模型性能会降低,因此,沙漏模型比延时模型的性能更稳定.Skabardonis 等人 [37] 将行程时间视为自由行
驶时间与交通信号延迟时间之和,使用基于运动波理论的排队论模型进行了预测.实验结果表明:在一个信号灯
周期内,预测行程时间与实际行程时间差异不超过 5%.Akiva 等人 [38] 提出了 DynaMIT 框架来预测交通状况.假
设预测时刻和当前时刻的交通状况类似,则预测结果是当前行程时间和过去行程时间的线性组合.由于该框架
使用过去一段时间的交通状况和当前时刻的实时数据对未来的交通状况进行预测,当未来交通状况发生变化
时,该模型的性能会降低.因此,这种方法只适用于交通状况未明显变化的情况,不适合长期预测.
(2) 细胞传输模型
1992 年,Daganzo 等人 [18] 提出了细胞传输模型(cell transmission model,简称 CTM).CTM 基于流体力学理论,
能根据选择的中间点描述和预测交通流.之后,CTM 被推广到交通网络 [39] ,并应用于高速公路和专用车道的研
究 [40] 以及交通仿真 [41] .CTM 的主要思想是:将道路划分为等长单元即“细胞”,同时,将时间离散化为等长的时间
间隔.细胞的长度等于车辆以自由流速在一个时间间隔内行驶的距离.车辆沿行驶方向从一个细胞驶入相邻的
另一个细胞.CTM 对于流量和密度之间的关系进行了分段线性化处理.当交通不拥堵时,上一个细胞的车辆数