Page 94 - 《软件学报》2020年第12期

3760 Journal of Software 软件学报 Vol.31, No.12, December 2020

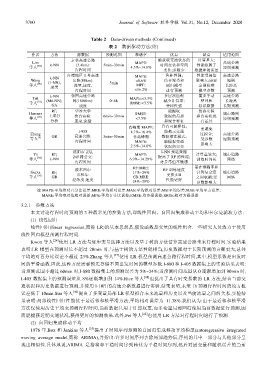
Table 2 Data-driven methods (Continued)
表 2 数据驱动方法(续)
作者 方法 源数据 预测范围 准确率 优点 缺点 适用范围
京釜高速公路 能获取交通状态的 计算量大;
Lim k-NN (3.4km): 5min~30min MAPE: 高速公路
等人 [89] 4.3%~14.8% 时间变化和空间 性能依赖于 短期预测
行程时间 变化;参数少 数据库的质量
台湾地区 1 号高速 MAPE: 鲁棒性强; 性能受阈值 高速公路
k-NN
Wang 公路(88km): <8.6% 结合聚类和 影响大;需要 短期
等人 [90] (1-NN), 流量,速度, 5min MPE: 回归模型 定期校准 长距离
聚类
行程时间 <16.2% 进行预测 模型参数 预测
k-NN 韩国高速公路 多层次匹配 需要手动 高速公路
Tak MAPE:<3.3%
等人 [91] (Mk-NN), 网(1800km): 0~6h RMSE:<3.5% 减少计算量; 整理和 长距离
GA 速度 鲁棒性强 标识数据 长期预测
RF, 华沙大学 能提取 仿真实验
Hamner 主成分 6min~30min RMSE: 城市路网
等人 [92] 仿真实验: <7.5% 数据的局部 和真实状况 短期预测
分析 速度,流量 和聚合特征 有差异
高峰期 MAPE: 具有可解释性;
I-95S 8.7%~18.4% 能揭示交通 要避免
Zhang 过拟合; 高速公路
[9]
等人 GB 高速公路: 5min~30min 非高峰期 数据潜在模式; 受参数 短期预测
行程时间 MAPE: 能捕捉交通
2.3%~14.8% 状况的突变 影响大
沈阳市 232, k-NN 预选数据
Yu RF, MAPE: 计算量较大; 城市道路
等人 [94] k-NN 249 路公交: 6.9%~14.29% 提高了 RF 的性能; 训练时间长 网络
行程时间 对异常值不敏感
RF:MRE: 需在准确率和
波尔图市 RF 训练速度
Gupta RF, 17%~29% 计算复杂度 城市道路
等人 [95] GB 出租车: GB:MRE: 更快;GB 之间权衡;受 网络
经纬度,速度 24%~29% 性能更好 参数影响大
注:MAPE:平均绝对百分比误差;MRE:平均相对误差;MAE:平均绝对误差;ME:平均误差;MSE:平均平方误差;
MARE:平均绝对值相对误差;MPE:平均百分比误差;RMSE:均方根误差;RRSE:相对方根误差
3.2.1 参数方法
本文讨论行程时间预测的 3 种最常见的参数方法,即线性回归、自回归集成移动平均和卡尔曼滤波方法.
(1) 线性回归
线性回归(linear regression,简称 LR)的基本思想是,假设函数是变量的线性组合.一些研究人员致力于使用
线性回归模型预测行程时间.
Kwon 等人 [24] 使用 LR 方法与逐步变量选择方法以及基于树的方法估算高速公路未来行程时间.实验结果
表明:LR 模型在预测时长不超过 20min 时,与基于树的方法性能相当,历史数据对于长期预测的贡献更大,总体
平均绝对百分比误差不超过 23%.Zhang 等人 [47] 使用 LR 模型预测高速公路行程时间,其中,模型系数是出发时
间的平滑函数.因此,这种方法需要预先存储不同出发时间的模型参数.I-880 和 I-405 数据集上的实验结果表明:
当预测范围不超过 60min 时,I-880 数据集上的预测误差为 5%~24%;当预测时间范围从 0 逐渐增加到 90min 时,
I-405 数据集上的预测误差从 8%逐渐增加到 14%.Rice 等人 [48] 也提出了具有时变系数的 LR 方法,结合当前交
通状况和历史数据进行预测,并使用 I-10E 的高速公路数据进行实验.结果表明,未来 1h 预测行程时间的均方根
误差低于 10min.Sun 等人 [49] 提出了多变量局部 LR 模型拟合未来流量和历史以及当前流量之间的关系,实验结
果表明:局部线性回归性能优于最近邻和核平滑方法,平均相对误差为 11.38%.我们认为:由于最近邻和核平滑
方法仅使用历史平均来预测行程时间,当前数据只用于计算权重,而多变量局部回归使用当前数据进行预测,因
而能捕获近期交通状况,获得更好的预测效果.此外,Fei 等人 [22] 也使用 LR 方法对行程时间进行了预测.
(2) 自回归集成移动平均
1976 年,Box 和 Jenkins 等人 [25] 提出了时间序列预测的自回归集成移动平均模型(autoregressive integrated
moving average model,简称 ARIMA),并指出:许多时间序列去除局部趋势后,序列的其中一部分与其他部分呈
现出相似性.具体地说,ARIMA 是指将非平稳时间序列转化为平稳时间序列,然后对因变量和随机误差的当前