Page 91 - 《软件学报》2020年第12期

柏梦婷 等:行程时间预测方法研究 3757

限制了流量;当交通拥堵时,下一个细胞的空间可用量限制了流量.
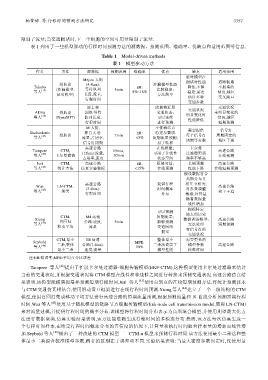
表 1 列出了一些模型驱动的行程时间预测方法的源数据、预测范围、准确率、优缺点和适用范围等信息.
Table 1 Model-driven methods
表 1 模型驱动方法
作者 方法 源数据 预测范围 准确率 优点 缺点 适用范围
延时模型在
Mejiro 大街 拥堵时性能 道路畅通
排队论 (4.4km): 沙漏模型性能
Takaba 等待队列 ER: 降低,不够 不拥堵的
等人 [17] (沙漏模型, 5min 5%~18% 比较稳定; 稳定;需要 情况;城区
延时模型) 长度,流量, 方法简单
行程时间 估计多种 交叉路口
交通参数
波士顿 能捕获近期 交通状况
Akiva 排队论 公路:等待 交通状态; 交通状况 未明显变化的
等人 [38] (DynaMIT) 队列长度, 可以连续 明显变化时 情况;城区
性能降低
行程时间 进行预测 短期预测
M 大街, 不依赖站点
Skabardonis 林肯大道: ER: 特定参数或 需要提供 信号灯
等人 [37] 排队论 流量,占用率, 7min <5% 短期流量预测; 每个信号灯 周期固定的
信号灯周期 易于转移 周期等参数 城区干道
高速公路 在线模型; 卡尔曼
Tampere CTM, (15km):流量, 15min, 可用于非线性 过滤器更新 高速公路
等人 [42] 卡尔曼滤波 30min 在线预测
占用率,速度 状态空间 频率不够高
Juri CTM, 高速公路 ER: 框架灵活; 长期预测 高速公路
等人 [43] 统计方法 仿真实验数据 <15% 在线预测 性能下降 在线短期预测
假设数据符合
高斯分布且
高速公路 提供行程 相互不相关;
Wan LN-CTM, (3.4km): 高速公路
等人 [45] 聚类 时间概率 对参数调整 和主干道
行程时间 分布 敏感;计算量
随着数据量
线性增加
根据特定
可以预测
CTM, M4 高速 短期流量; 地点的历史
Xiong 数据训练模型; 高速公路
等人 [44] 自回归 公路:速度, 5min 能够预测 无法处理 短期预测
移动平均 流量 交通网络 有信号灯的
拥塞
交通状况
CTM,最小 E4 高速 整体最小 需要更长的
Seybold MPE:
等人 [46] 二乘,整体 公路(7.4km): 19% 二乘法提高了 模型参数 高速公路
最小二乘 速度,流量 模型性能 校准时间
注:ER:错误率;MPE:平均百分比误差
Tampere 等人 [42] 提出了扩展卡尔曼过滤器-细胞传输模型(EKF-CTM),这种模型使用卡尔曼过滤器来估计
当前的交通状况,并根据交通状况将 CTM 模型在线性和非线性之间进行转换来预测交通状况.高速公路仿真结
果表明,该模型能捕获拥塞并预测短期行程时间.Juri 等人 [43] 使用点到点的在线短期预测方法,将统计预测技术
与 CTM 交通仿真相结合,使用滑动窗口框架进行在线行程时间预测.Xiong 等人 [44] 建立了一个三级结构的 CTM
模型,使用自回归集成移动平均方法进行高速公路的短期流量预测,根据预测流量和 N 曲线分析预测短期行程
时间.Wan 等人 [45] 使用基于随机模型的链路节点细胞传输模型(link-node cell transmission model,简称 LN-CTM)
来对流量建模,并提供行程时间的概率分布.该模型将行程时间分布表示为高斯混合模型,并使用期望最大化方
法进行数据聚类.仿真实验结果表明,该方法能准确生成行程时间的多模态分布.然而,该方法每次仿真生成一
个行程时间样本,在给定行程时间概率分布的置信度的情况下,计算量和执行时间随着样本量的增加而线性增
加.Seybold 等人 [46] 提出了一种改进的 CTM 模型——CTM-u 模型来预测行程时间.该方法使用最小二乘法和整
体最小二乘拟合校准模型参数,两者的区别在于误差项不同.实验结果表明:当最大密度参数固定时,仅使用最