Page 84 - 《软件学报》2020年第12期

3750 Journal of Software 软件学报 Vol.31, No.12, December 2020

比较表 5~表 7 中各算法的 DR 值,MCC-NES 在 Cleveland,Wine,Vehicle,Segmentatin,Dermatology,Musk2,
SRBCT,RNA-Seq 和 Dorothea 数据集上有最高的维度压缩率.对于其他的数据集,虽然不能在所有分类器上达到
最高,但是 MCC-NES 的 DR 值仍具有很强的竞争力,特别是在处理高维数据时,在 Ionosphere 数据集 70%-30%
划分条件下,分类器为 CART 时,MCC-NES 要比效果最好的 FSFOA 算法高出较接近 40%;在 Arcene 数据集 70%-
30%划分条件下,分类器为 1-NN 时,MCC-NES 比次优 DR 的算法高出 36%;在 RNA-Seq 的 1-NN 分类器下,MCC-
NES 的 DR 值高出 Rc-BBFA 算法 40%;在 Dorothea 的 CART 分类器下,MCC-NES 的 DR 值高出 FSFOA 算法
70%.
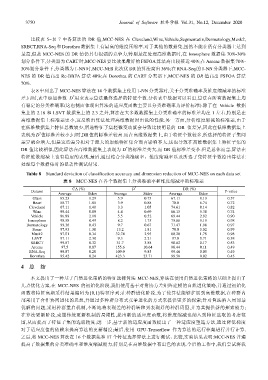
表 8 中列出了 MCC-NES 算法在 14 个数据集上使用 1-NN 分类器时,关于分类准确率及维度缩减率的标准
*
差.同时,表中添加参数 D 用来表示算法最终选择的特征个数.分析表中数据可以看出,算法在所有数据集上均
有稳定的分类准确率(这也侧面体现出算法的适应度函数主要以分类准确率为评价标准).除了在 Vehicle 数据
集上的 2.18 和 LSVT 数据集上的 2.3 之外,算法在大多数数据集上分类准确率的标准差均在 1 左右,特别是在
高维数据集上标准差更小,这反映出算法处理高维数据时出色的性能.另一方面,分析维度缩减的标准差,由于
在低维数据集上特征总数较少,所选特征子集轻微变动就会导致比较明显的 DR 值差异,因此在低维数据集上
*
表现为 D 值标准差较小;同时,DR 值的标准差较高.而在高维数据集上,由于特征个数较多,所选择的特征子集间
差异就会增大,但是这些差异相对于庞大的原始特征集合而言影响不大,这也导致在高维数据集上特征子集的
*
DR 值比较相似,因此算法在高维数据集上表现为 D 的标准差变大,而 DR 值标准差变小.但是总体而言,算法在
特征维数缩减上也有稳定的表现.最后,通过结合分类准确率、维度缩减率以及所选子集特征个数给出算法在
处理每个数据集时的显著性测试结果.

Table 8 Standard deviation of classification accuracy and dimension reduction of MCC-NES on each data set
表 8 MCC-NES 在各个数据集上分类准确率和维度缩减率的标准差
*
CA (%) D DR (%)
Dataset P-value
Average Stdev Average Stdev Average Stdev
Glass 85.23 1.29 5.9 0.73 67.11 8.19 0.57
Heart 88.77 1.08 3.9 0.88 70.0 6.74 0.72
Cleveland 67.11 1.40 3.3 1.05 74.61 8.14 0.82
Wine 99.44 0.89 4.4 0.69 66.15 5.38 0.74
Vehicle 86.89 2.18 5.5 0.52 69.44 2.92 0.90
Ionosphere 98.58 0.49 8.2 1.75 75.88 5.15 0.98
Dermatology 99.36 0.43 9.7 0.67 71.47 1.98 0.97
Sonar 97.93 1.30 13.2 1.81 78.0 3.02 0.99
Musk2 97.01 0.34 32.74 2.95 80.28 1.78 0.98
LSVT 97.11 2.30 9.3 2.21 97.0 0.71 0.38
SRBCT 99.87 0.32 31.7 3.88 98.62 0.17 0.53
Arcene 97.5 0.87 155.6 10.64 98.44 0.11 0.49
RNA-Seq 99.87 0.20 109.9 9.85 99.46 0.05 0.49
Dorothea 95.42 0.24 423.3 23.71 99.58 0.02 0.45
4 总 结

本文提出了一种基于自然进化策略的特征选择算法 MCC-NES,算法在使用自然进化策略的基础上提出了
几点优化方案.在 MCC-NES 的初始化阶段,我们使用基于对角协方差矩阵建模的自然进化策略,并通过初始化
函数将特征高斯采样结果编码为{0,1}特征序列;在种群进化阶段,为了使算法能够扩展到高维数据,在种群内
部采用了合作协同进化的思想,并通过多种群分布式竞争进化的方式来提供更多的探索;针对算法陷入局部最
优解的问题,采用种群重启机制,不断地将表现差的种群转移到表现好的种群周围,并为其提供新的探索能力;
在算法更新阶段,克服传统更新机制的局限性,提出新的适应度函数,将维度缩减也纳入到特征选取的考虑范
围,从而提高了特征子集的选取精度;进一步,基于新的适应度函数提出了一种适应度塑造方法,通过降低梯度
对于适应度值的依赖来提高算法的更新精度;最后,使用 GPU-Tensorflow 作为算法的运行框架进行并行计算.
之后,将 MCC-NES 算法在 16 个数据集和 17 个特征选择算法上进行测试、比较,实验结果表明:MCC-NES 普遍
提高了数据集的分类准确率和维度缩减能力,特别是在高维数据中有出色的表现.今后的工作中,我们尝试将我