Page 416 - 《软件学报》2025年第12期

李洁 等: 历史交通数据驱动的 VANET 智能路由算法 5797

如表 1 所示, 在时间复杂度方面, 3 个对比算法的时间复杂度均为 O(|VR |), 这主要是因为, 对于 QGrid-M 来
t
O(|VR |). 对于 QGrid-G 和
t
说, 需计算所有邻居的位置转移概率来选择最优的下一邻居, 所以, 时间复杂度约为
t
W-PAGPSR 来说, 均需要计算所有邻居节点与目的地的距离来选择最优的下一邻居, 因此, 其时间复杂度亦为 O(|VR |).
而由第 3.2.3 节计算时间复杂度分析可知, 本文算法 HTD-IR 的时间复杂度为 O(|C |), 所以, 本文算法在线阶段的
t
时间复杂度优于其他 3 种路由算法. 图 19 的仿真结果进一步验证了这一结论.
图 19 展示了不同车辆数量和传输半径 R 下, 各算法的执行时间变化趋势. 结果表明, 所有算法的执行时间均
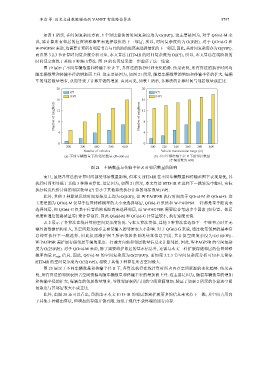
随车辆数量和传输半径的增加而上升. 这主要是因为, 如图 21 所示, 随着车辆数量的增加和传输半径的扩大, 每辆
车的邻居数量增多, 从而导致了计算开销的增加. 由此可见, 如表 1 所示, 各算法的计算时间与邻居数量成正比.

20 20
|C | t |C | t
|VR | t |VR | t
16 16
Number of neighbors 12 8 Number of neighbors 12 8

4 4

0 0
200 300 400 500 600 300 320 340 360 380 400
Number of vehicles Vehicle transmission range (m)
(a) 不同车辆数量下的邻居数量 (R=360 m) (b) 不同车辆传输半径 R 下的邻居数量
(车辆总数为 600)
图 21 车辆数量与传输半径 R 对邻居数量的影响

而且, 虽然各算法的计算时间都受邻居数量影响, 但本文 HTD-IR 在不同车辆数量和传输范围下表现最优, 其
执行时间明显低于其他 3 种路由算法. 这是因为, 如图 21 所示, 本文算法 HTD-IR 在选择下一跳转发中继时, 实际
t t
执行转发代价计算的邻居数量 |C | 要小于其他算法执行计算的邻居数量 |VR |.
此外, 其他 3 种算法虽然时间复杂度上均为 O(|VR |), 但 W-PAGPSR 执行时间高于 QGrid-M 和 QGrid-G. 这
t
主要是因为 QGrid-M 仅基于位置转移概率的大小来选择邻居, QGrid-G 虽然和 W-PAGPSR 一样都是基于距离来
选择邻居, 但 QGrid-G 仅基于位置的欧氏距离来选择邻居, 而 W-PAGPSR 需要综合考虑多个因素 (如位置、邻居
密度和通信链路质量等) 来计算邻居. 因此 QGrid-M 和 QGrid-G 计算量较小, 执行速度更快.
表 2 展示了各算法在线计算的空间复杂度情况. 与本文算法类似, 其他 3 种算法在选择下一中继节点时并无
额外的数据结构引入, 其空间复杂度亦主要受输入的邻居表大小影响. 对于 QGrid-G 来说, 通过收集邻居的基本信
息即可执行下一跳选择, 因此仅需维护图 7 所示邻居条目的基本信息字段, 其计算空间复杂度为 O(18|VR |).
t
W-PAGPSR 需扩展存储邻居车辆的速度、行驶方向角和邻居数量信息来计算邻居, 因此, W-PAGPSR 的空间复杂
O(23|VR |). 对于 QGrid-M 来说, 除了需要维护邻居的基本信息外, 还需与本文一样扩展存储邻居的位置转移
t
度为
t
概率向量 P neigh 信息, 因此, QGrid-M 的空间复杂度为 O(27|VR |). 而如第 3.2.3 节空间复杂度分析可知本文算法
t
HTD-IR 的空间复杂度为 O(32|VR |), 相较于其他 3 种算法所占空间最大.
图 20 展示了不同车辆数量和传输半径 R 下, 各算法执行在线计算时所占内存空间资源的变化趋势. 结果表
明, 所有算法的邻居表所占空间资源均随车辆数量和传输半径的增加而上升. 这主要是因为, 随着车辆数量的增加
和传输半径的扩大, 每辆车的邻居数量增多, 导致邻居表所占用的空间资源增加, 验证了如表 2 所示的各算法空间
复杂度与其邻居表大小成正比.
此外, 由图 20 还可以看出, 虽然由于本文 HTD-IR 的邻居表需扩展更多的信息来支持下一跳, 其空间占用高
于其他 3 种路由算法, 但增加的存储开销有限, 远低于现代车载终端的运行内存.