Page 176 - 《软件学报》2025年第9期

李文艺 等: 增量构造式随机循环神经网络 4087

T
表示为一个动态系统的形式 y(t) = g(y(t −1), x(t)), 其中 x(t) = [x 1 (t), x 2 (t), x 3 (t), x 4 (t), x 5 (t)] . 考虑到实际工程条件,
每隔 30 min 采集水泥熟料进行化验, 再经过线性插值得到间隔为 10 min 的 f-CaO 含量的数据, 同时按照
10 min 间隔采集对应的辅助变量. 经数据采集和插值处理后得到 f-CaO 含量正常、偏大、偏小的数据分别是
1 000 组、200 组、200 组. 从正常、偏低、偏大的数据中按照时间先后顺序分别取相邻的 100 组、35 组、40 组
数据作为测试集, 其余的数据作为训练集.
采用归一化之后的数据对单层 LSTM, 单层 RNN, ESN, GESN 与本文方法进行训练与测试. LSTM 与 RNN 的
隐含节点个数都设定为 100, epoch=300, 采用 Adam 算法优化参数, 学习速率都为 0.000 5. ESN, GESN 与 PDSM-
−8
,
,
,
,
ESN 的参数设置与算例 3 相同. 在算法 IR-1 与 IR-2 中 L max = 200 C max = 10 ε = 0.015 r = 1×10 , λ W = 1.5 λ W in =
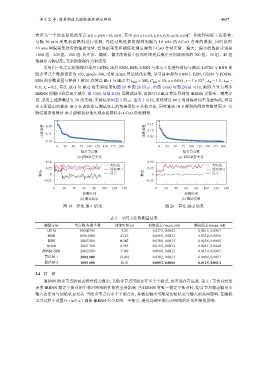
0.8, λ b = 0.2. 算法 IR-1 与 IR-2 的实验结果如图 19 和图 20 所示. 由图 19(a) 与图 20(a) 可知, 随隐含节点增多
IRRNN 的输出误差逐步减少. 图 19(b) 与图 20(b) 是测试结果, 由图可知 IR-2 算法得到的 IRRNN 更紧凑、精度更
高. 采用上述参数进行 50 次实验, 实验结果如表 5 所示. 由表 5 可知, 虽然算法 IR-2 的训练时间不是最短的, 但是
本文所提出的算法 IR-2 在训练集与测试集上的效果要优于其他方法, 同时算法 IR-2 得到的网络参数量更少. 实
验结果表明算法 IR-2 能够较好地实现水泥熟料中 f-CaO 的软测量.

0.15
训练误差 0.15 训练误差 0.10
0.20

0.10 0.05
0 25 50 75 100 125 150 175 200 0 25 50 75 100 125 150 175 200
隐含节点数 隐含节点数
(a) 训练误差变化 (a) 训练误差变化
0.50 0.50
实际值 实际值
0.25 算法IR-1 0.25 算法IR-2
输出 0 误差 输出 0 误差
−0.25 −0.25

0 20 40 60 80 100 120 140 0 20 40 60 80 100 120 140
检测时刻 检测时刻
(b) 测试结果 (b) 测试结果
图 19 算法 IR-1 结果 图 20 算法 IR-2 结果

表 5 不同方法软测量结果

测量方法 节点数/参数个数 训练时间 (s) 训练误差 (mean, std) 测试误差 (mean, std)
LSTM 100/42 901 3.25 0.037 2, 0.004 2 0.081 5, 0.006 7
RNN 100/10 801 27.15 0.029 9, 0.003 1 0.035 2, 0.003 6
ESN 200/5 200 0.167 0.018 0, 0.001 5 0.025 6, 0.004 5
GESN 200/1 700 0.353 0.010 2, 0.001 2 0.026 1, 0.004 4
PDSM-ESN 200/2 200 3.389 0.009 8, 0.001 2 0.015 4, 0.004 7
算法IR-1 200/1 600 18.461 0.038 2, 0.001 3 0.040 9, 0.003 7
算法IR-2 200/1 600 16.41 0.009 2, 0.000 6 0.012 5, 0.002 4

3.4 讨 论
IRRNN 隐含节点的动态特性较为复杂, 其隐含节点可能存在多个平衡点, 也可能存在震荡. 第 3.1 节仿真结果
表明 IRRNN 稳定平衡点的个数对网络的性能有重要影响. 当 IRRNN 有唯一稳定平衡点时, 隐含节点稳态输出由
输入决定而与初始状态无关. 当隐含节点有多个平衡点时, 其稳态输出可能受初始状态与输入的共同影响. 在随机
in
学习过程中设置 0 < |w | ⩽ 1 确保 IRRNN 有全局唯一平衡点, 避免局部平衡点对网络的泛化性能的影响.