Page 171 - 《软件学报》2025年第9期

4082 软件学报 2025 年第 36 卷第 9 期

1.00
初始状态=−0.95 1.00 A: 稳态输出
0.75 初始状态=−0.57 0.75
初始状态=−0.19
0.50
初始状态=0.19 0.50
0.25 初始状态=0.57 0.25 初始状态=−0.95
初始状态=−0.57
输出 0 初始状态=0.95 输出 0 初始状态=−0.19
−0.25 −0.25 初始状态=0.19
初始状态=0.57
−0.50 −0.50 初始状态=0.95
−0.75 稳态输出 −0.75 B: 稳态输出
−1.00 −1.00
0 5 10 15 20 25 30 0 5 10 15 20 25 30
时刻 时刻
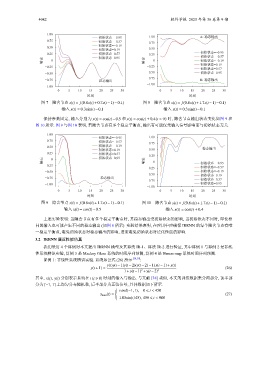
图 7 隐含节点 s(t) = f(0.8x(t)+0.7s(t −1)−0.1) 图 8 隐含节点 s(t) = f(0.8x(t)+1.7s(t −1)−0.1)
x(t) = 0.3sin(t)−0.1 x(t) = 0.3sin(t)−0.1
输入 输入
(
保持参数固定, 输入分别为 x(t) = cos(t)−0.5 和 x(t) = cos(t) + 0.4 t > 0) 时, 隐含节点输出状态变化如图 9 和
图 10 所示. 图 9 与图 10 表明, 若隐含节点有多个稳定平衡点, 输出有可能仅受输入信号影响而与初始状态无关.

1.00
初始状态=−0.95 1.00
0.75 初始状态=−0.57
初始状态=−0.19 0.75
0.50 稳态输出
初始状态=0.19 0.50
0.25 初始状态=0.57 0.25
输出 0 初始状态=0.95 输出 0 初始状态=−0.95
−0.25
−0.25 初始状态=−0.57
−0.50 初始状态=−0.19
−0.50 初始状态=0.19
−0.75 稳态输出
−0.75 初始状态=0.57
−1.00 初始状态=0.95
−1.00
0 5 10 15 20 25 30 0 5 10 15 20 25 30
时刻 时刻
图 9 隐含节点 s(t) = f(0.8x(t)+1.7s(t −1)−0.1) 图 10 隐含节点 s(t) = f(0.8x(t)+1.7s(t −1)−0.1)
输入 x(t) = cos(t)−0.5 输入 x(t) = cos(t) + 0.4
上述实验表明: 当隐含节点有多个稳定平衡点时, 其稳态输出受初始状态的影响, 当初始状态不同时, 即使相
同的输入也可能产生不同的稳态输出 (如图 8 所示). 实验结果表明, 在应用中应确保 IRRNN 的每个隐含节点有唯
一稳定平衡点, 避免初始状态对稳态输出的影响, 进而避免初始状态对泛化性能的影响.

3.2 IRRNN 逼近性能仿真
我们采用 4 个算例对本文提出 IRRNN 模型及其算法 IR-1、算法 IR-2 进行验证, 其中算例 1 与算例 2 是非线
性系统辨识实验, 算例 3 是 Mackey Glass 系统的时间序列预测, 算例 4 是 Henon map 系统时间序列预测.
算例 1: 非线性系统辨识实验. 系统如公式 (26) 所示 [38,39] :

y(t)y(t −1)y(t −2)(y(t −2)−1)x(t −1)+ x(t)
y(t +1) = (26)
2
1+y(t −1) +y(t −2) 2
其中, x(t) y(t) 分别表示系统在 t (t ⩾ 0) 时刻的输入与输出. 与文献 [38] 类似, 本文的训练数据集分两部分, 前半部
,
分为 [−1, 1] 上均匀分布随机数, 后半部分为正弦信号, 具体数据如下所示.


 rand(−1,1), 0 ⩽ t < 450


x train (t) =  (27)

 1.05sin(t/45), 450 ⩽ t < 900