Page 170 - 《软件学报》2025年第9期

李文艺 等: 增量构造式随机循环神经网络 4081

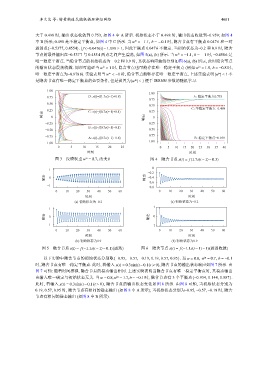
大于 0.498 时, 输出状态收敛到 0.753, 如图 4 中 A 所示. 初始状态小于 0.498 时, 输出状态收敛到−0.959; 如图 4
in
中 B 所示; 0.498 是不稳定平衡点, 如图 4 中 C 所示. 当 w = −1.1 b = −0.1 时, 隐含节点有平衡点 0.047 6 和一对
,
震荡点{−0.5377, 0.4554}. | f (−0.0476)| = 1.098 > 1, 因此平衡点 0.047 6 不稳定. 当初始状态为−0.2 和 0.9 时, 隐含
′
in
节点的最终输出在−0.537 7 与 0.455 4 两点之间产生震荡, 如图 5(a), (b) 所示. 当 w = −1.1 b = −1 时, −0.458 6 是
,
− 0.2 和 0.9 时, 其状态响应曲线分别如图 6(a), (b) 所示, 此时隐含节点
唯一稳定平衡点. 当隐含节点的初始状态为
in
in
的输出状态震荡收敛. 同理可验证当 w > 1 时, 隐含节点也可能存在唯一稳定平衡点 (例如 w = 1.5, b = −0.8 时,

in |w | < 1 不
in
唯一稳定平衡点为−0.978 8). 实验表明当 w < −1 时, 隐含节点能够存在唯一稳定平衡点. 上述实验表明
in
是隐含节点有唯一稳定平衡点的必要条件, 但是设置为 |w | < 1 便于 IRRNN 参数的随机学习.

1.00
1.00
D: s(t)=f(1.7s(t−1)+0.8) A: 稳定平衡点0.753
0.75
0.75
0.50
0.50
0.25 C: s(t)=f(0.7s(t−1)+0.1) 0.25 C: 不稳定平衡点−0.498
输出 0 输出 0
−0.25 −0.25
B: s(t)=f(0.7s(t−1)−0.1)
−0.50 −0.50
−0.75 A: s(t)=f(0.7s(t−1)−0.8) −0.75 B: 稳定平衡点−0.959
−1.00 −1.00
0 5 10 15 20 25 0 5 10 15 20 25 30 35 40
时刻 时刻
in
图 3 反馈权重 w = 0.7, 改变 b 图 4 隐含节点 s(t) = f(1.7s(t −1)−0.3)

0

1
输出 0 输出 −0.2
−0.4
−0.6
−1 −0.8
0 10 20 30 40 50 60 0 10 20 30 40 50 60
时刻 时刻
(a) 初始状态为−0.2 (a) 初始状态为−0.2
1
1
输出 0 输出 0
−1 −1
0 10 20 30 40 50 60 0 10 20 30 40 50 60
时刻 时刻
(b) 初始状态为0.9 (b) 初始状态为0.9

图 5 隐含节点 s(t) = f(−1.1s(t −1)−0.1)(震荡) 图 6 隐含节点 s(t) = f(−1.1s(t −1)−1)(震荡收敛)
in
,
以下实验中隐含节点的初始状态分别取{−0.95, −0.57, −0.19, 0.19, 0.57, 0.95}. 当 w = 0.8, w = 0.7 b = −0.1

x(t) = 0.3sin(t)−0.1 t ⩾ 0), 隐含节点的输出状态响应如图 7 所示. 由
(
时, 隐含节点有唯一稳定平衡点. 此时, 若输入
图 7 可知: 随着时间推移, 隐含节点的稳态输出相同. 上述实验表明当隐含节点有唯一稳定平衡点时, 其稳态输出
in
由输入唯一确定与初始状态无关. 当 w = 0.8,w = 1.7,b = −0.1 时, 隐含节点有 3 个平衡点{−0.934, 0.144, 0.887}.
(
此时, 若输入 x(t) = 0.3sin(t)−0.1 t > 0), 隐含节点的输出状态变化如图 8 所示. 由图 8 可知, 当初始状态分别为
0.19, 0.57, 0.95 时, 隐含节点有相同的稳态输出 (如图 8 中 A 所示); 当初始状态分别为−0.95, −0.57, −0.19 时, 隐含
节点有相同的稳态输出 (如图 8 中 B 所示).