Page 180 - 《软件学报》2025年第9期

李文艺 等: 增量构造式随机循环神经网络 4091

a 是激活函数 f 的平衡点. 若 f(a) = b , a, 则:
f(f(a)) = f(b) = a (A2)

又有 f(a) = b, 因此 a, b 构成一组震荡点. 综上所述 f(f(s)) = s 的解是隐含节点的平衡点或震荡点. 证毕.

1.00 C
0.75
0.50
l 3
0.25 B
输出s(t) 0 D (0, 0) M l 1 l 2 : w >0
in
−0.25
in
l 3 : w <0
−0.50 l 1
−0.75
A l 2
−1.00
−1.00 −0.75 −0.50 −0.25 0 0.25 0.50 0.75 1.00
输入s(t−1)
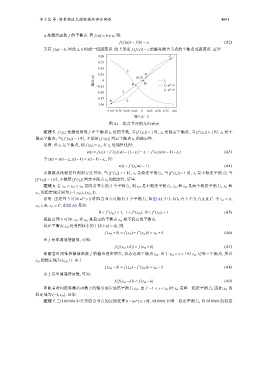
图 A1 隐含节点的几何表示

定理 5. f (s e ) 是激活函数 f 在平衡点 s e 处的导数, 当 |f (s e )| < 1 时, s e 是稳定平衡点; 当 |f (s e )| > 1 时, s e 是不
′
′
′
′ ′
稳定平衡点; 当 |f (s e )| = 1 时, 不能用 |f (s e )| 判定平衡点 s e 的稳定性.
证明: 若 s e 是平衡点, 则 f(s e ) = s e , 在 s e 处线性化得:

′
s(t) ≈ f(s e ) + f (s e )(s(t −1)− s e ) = s e + f (s e )(s(t −1)− s e ) (A3)
′
令 z(t) = s(t)− s e ,z(t −1) = s(t −1)− s e , 得:

′
z(t) = f (s e )z(t −1) (A4)
′
′
由离散系统稳定性判别方法可知, 当 | f (s e )| < 1 时, s e 是稳定平衡点, 当 | f (s e )| > 1 时, s e 是不稳定平衡点; 当
′ ′ s e 的稳定性. 证毕.
|f (s e )| = 1 时, 不能用 |f (s e )| 判定平衡点
定理 6. 若 s e1 < s e2 < s e3 是隐含节点的 3 个平衡点, 则 s e2 是不稳定平衡点, s e1 和 s e3 是两个稳定平衡点, s e1 和
,
s e1 的稳定域分别为 (−1, s e2 ) (s e2 ,1).
证明: 由定理 3 可知 w > 1 时隐含节点可能有 3 个平衡点, 如图 A1 中 l 1 与 l 2 有 3 个交点 A,B,C. 令 s e1 = A,
in
s e2 = B s e3 = C, 由图 A1 易知:
,

′
0 < f (s e1 ) < 1, 1 < f (s e2 ), 0 < f (s e3 ) < 1 (A5)
′
′
根据定理 5 可知: s e1 和 s e3 是稳定的平衡点 s e2 是不稳定的平衡点.

设在平衡点 s e2 处受到较小的干扰 δ (δ > 0), 则:
f(s e2 +δ) ≈ f(s e2 )+ f (s e2 )δ > s e2 +δ (A6)
′
由 f 是单调递增函数, 可知:

f(f(s e2 +δ)) > f(s e2 +δ) (A7)
即随着时间推移激活函数 f 的输出逐步增大, 状态远离平衡点 s e2 . 由于 s e2 < s < 1 时 s e3 是唯一平衡点, 所以
(s e2 ,1). 由于
s e3 的稳定域为

′
f(s e2 −δ) ≈ f(s e2 )− f (s e2 )δ < s e2 −δ (A8)
由 f 是单调递增函数, 可知:
f(f(s e2 −δ)) < f(s e2 −δ) (A9)
x e1 的
即随着时间推移激活函数 f 的输出逐步远离平衡点 s e2 . 由于 −1 < s < s e2 时 x e1 是唯一稳定平衡点, 因此
(−1, s e2 ). 证毕.
稳定域为
定理 7. 当 IRRNN 中任意隐含节点的反馈权重 0 < |w | ⩽ 1 时, IRRNN 有唯一稳定平衡点, 且 IRRNN 的稳态
in