Page 18 - 《软件学报》2025年第8期

谭思危 等: Fast-USYN: 从酉矩阵到高质量量子电路的快速合成 3441

于计算成本高, 这些方法无法扩展到更大数量的量子比特. QuCT [19] 是最近的一种量子电路合成方法, 它采用数据
驱动的方法来加速搜索, 相比于最优量子程序, 它合成的程序仍然会包含 3 倍以上的门. Bocharov 等人 [26] 使用重
复迭代电路进行近似. 一些方法针对特定类型的酉矩阵设计了合成方法, 如 Clifford 酉矩阵 [27] 和稀疏酉矩阵 [28] .
Peham 等人 [29] 提供了一种检验电路等效性的范例, 但该方法不能比较参数化电路的等价性, 无法用于酉矩阵合成
中. 与之前的方法相比, Fast-USYN 通过重新设计合成的关键阶段提供了显著的加速和门数量优化. Kang 等人 [11]
提出了利用模块化的量子电路组成合成量子程序, 但是该方法难以合成任意酉矩阵. Paradis 等人 [20] 则提出了基于
模拟退火的方法合成电路, 但是该方法难以应用于超过 4 量子比特的随机酉矩阵的合成. Li 等人 [30] 提出了一种基
于强化学习的门优化算法, 可以帮助合成电路降低量子门的数量.

2.1 0.24 15
175
1.9 0.22 150
门数量优化倍数 1.5 0.20 合成时间 (h) 候选电路模块数量 125 10 加速比
1.7
100
0.18
75
0.16
1.3
1.1 0.14 50 5
25
0.9 0.12 5 0
1 2 3 4 5 50 60 70 80 90 100
搜索深度 覆盖阈值 (%)
门数量优化倍数 合成时间 (h) 候选电路模块数量 加速比
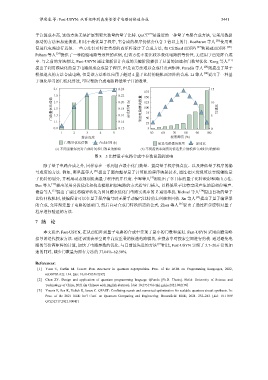
(a) 不同前瞻深度对合成时间和门数量的影响 (b) 不同覆盖率阈值对候选集合规模和合成时间的影响
图 8 5 比特量子电路合成中参数设置的影响

除了量子电路合成之外, 同样存在一系列旨在最小化门数量、提高量子程序保真度、以及降低量子程序的编
写难度的方法. 例如, 窦星磊等人 [31] 提出了面向超导量子计算机的程序映射技术, 通过社区发现算法实现辅助量
子比特的划分, 并利用动态规划提高量子程序的并行度. 李晖等人 [4] 则提出了多目标的量子比特映射和路由方法.
Das 等人 [32] 提出采用分段优化和构造模拟相似电路的方式指导门插入, 以降低量子比特空闲产生的退相位噪声.
谢磊等人 [33] 提出了通过将编译转化为图问题来优化门电路实现中的 Z 通道串扰. Bichsel 等人 [34] 提出自动的量子
比特回收机制, 使编程者可以在量子程序编写时无需手动编写比特的去纠缠和回收. Xu 等人 [35] 提出了量子编译器
的合成, 允许指定量子电路的基础门, 然后自动合成门转换所需的公式. Zhou 等人 [36] 提出了通过霍尔逻辑对量子
程序进行验证的方法.

7 结 论

本文提出 Fast-USYN, 在从酉矩阵到量子电路的合成中实现了最小的门数和延迟. Fast-USYN 采用前瞻策略
指导的迭代搜索方法. 通过识别表示空间中高度重叠的候选电路模块, 在搜索中对搜索空间进行剪枝. 通过避免电
路的等价酉矩阵的计算, 加快了电路参数的优化. 与目前最先进的方法 [19] 相比, Fast-USYN 实现了 3.7–20.6 倍的加
速的同时, 减少门数量为原有方法的 37.04%–62.50%.

References:
[1] Yuan C, Carbin M. Tower: Data structures in quantum superposition. Proc. of the ACM on Programming Languages, 2022,
6(OOPSLA2): 134. [doi: 10.1145/3563297]
[2] Chen ZY. Design and application of quantum programming language QPanda [Ph.D. Thesis]. Hefei: University of Science and
Technology of China, 2021 (in Chinese with English abstract). [doi: 10.27517/d.cnki.gzkju.2021.002170]
[3] Younis E, Sen K, Yelick K, Iancu C. QFAST: Conflating search and numerical optimization for scalable quantum circuit synthesis. In:
Proc. of the 2021 IEEE Int’l Conf. on Quantum Computing and Engineering. Broomfield: IEEE, 2021. 232–243. [doi: 10.1109/
QCE52317.2021.00041]