Page 181 - 《软件学报》2024年第4期

赵文竹 等: 多视角融合的时空动态 GCN 城市交通流量预测 1759

O
MultiHead(Q,K,V)=Concat(head 1 ,…,head h )W (6)
head = Attention (QW i Q ,KW i K ,VW i V ) (7)
i
V
O
其中, h 代表注意力模块(头)的数量, W i Q , W i K , W 分别代表在 Q, K, V 上的投影矩阵, W 代表最终输出的投
i
影矩阵, Concat 代表拼接操作. 多头自注意力机制可以充分考虑序列中不同位置之间的关系, 允许建模序列
中元素的相关性, 从而更好地捕获交通数据中长期依赖关系, 通过堆叠多个自注意力层来学习不同层次的特
征表示, 有效捕捉交通数据中的复杂模式和动态关系, 实现精准的交通长期预测.
交通序列模式会随时间显著地演变, 且易受节假日、交通事故、极端天气等事件影响. 因此, 判断观测点
是寻常模式还是存在异常, 需要充分结合路网局部结构信息. 传统的多头自注意力机制在自然语言处理领域
用于处理离散的标记序列, 因此, 自注意力模块中查询和键之间的相似度是基于点值计算, 忽略了形状、趋势
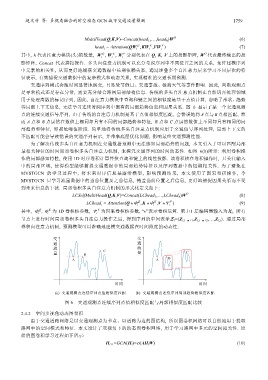
等局部上下文信息, 无法学习连续时间序列中固有的局部趋势信息和因果关系. 图 6 显示了某一个交通观测
点的连续交通信号序列, 由于传统的自注意力机制是基于点值相似度匹配, 会错误地将 A 点与 B 点相匹配, 然
而 A 点和 B 点虽然在数值上相同却具有不同的局部趋势和特征, B 点和 C 点虽然数值上不同却具有相同的局
部趋势和特征, 即都处峰值阶段. 简单地将传统多头自注意力机制应用于交通信号序列处理, 局部上下文的
不匹配可能会导致错误的交通序列表示, 并带来底层优化问题, 影响最终交通预测性能.
为了解决传统多头自注意力机制在交通数据预测中无法感知局部趋势的问题, 本文引入了可以匹配局部
最相关特征的时间局部卷积多头自注意力机制, 来探究交通序列的时间动态性. 如图 6(b)所示: 利用卷积操
作的局部感知特性, 使用 1D 时序卷积计算替换查询和键上的线性投影. 该卷积核在卷积操作时, 只关注输入
中的局部区域, 使得模型能够捕捉交通数据中的局部趋势特征以及序列数据中的短期相关性. 为了避免在
MVSTGCN 的学习过程中, 将未来时序信息暴露给模型, 影响预测结果, 本文使用了因果卷积操作, 令
MVSTGCN 只学习流量数据中的当前位置及之前信息, 掩盖当前位置之后信息, 更好地捕捉因果关系而不受
到未来信息的干扰. 局部卷积多头自注意力机制的形式化定义如下:
O
LCSelfMultiHead(Q,K,V)=Concat(LChead 1 ,…,LChead h )W (8)
LChead = Attention Q Φ i Q ,K  Φ i K ,V  Ψ i V ) (9)
( 
i
V
其中, Φ i Q , Φ i K 为 1D 卷积核参数, Ψ 为因果卷积核参数, “”表示卷积运算. 第 l+1 层编码器输入为 l , 所有
i
节点上进行时间局部卷积多头自注意力操作之后, 得到序列的中间表示 l =(Z l,t−m+1 ,Z l,t−m+2 ,…,Z l,t ). 通过局部
卷积自注意力机制, 预测模型可以准确地建模交通数据在时间维度的动态性.

交 交
通 通
流 流
量 量

时间 时间
(a) 交通观测点连续序列点值相似度匹配 (b) 交通观测点连续序列局部趋势相似度匹配
图 6 交通观测点连续序列点值相似度匹配与局部相似度匹配比较

2.4.2 空间多视角动态图卷积
由于交通道路网络是以交通观测点为节点、以道路为边的图结构, 所以图卷积网络可以自然地用于提取
路网中的空间模式和特征. 本文设计了双视角下的动态图卷积网络, 用于学习路网中多元的空间相关性. 原
始的图卷积学习过程如下所示:
H l+1 =GCN(H l )=s(AH l W) (10)