Page 185 - 《软件学报》2024年第4期

赵文竹 等: 多视角融合的时空动态 GCN 城市交通流量预测 1763

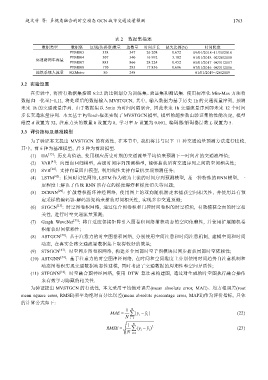
表 2 数据集描述
数据类型 数据集 区域(传感器)数量 边数量 时间步长 缺失比例(%) 时间跨度
PEMS03 358 547 26 208 0.672 09/01/2018−11/30/2018
PEMS04 307 340 16 992 3.182 01/01/2018−02/28/2018
高速路网车流量
PEMS07 883 866 28 224 0.452 05/01/2017−08/31/2017
PEMS08 170 295 17 856 0.696 07/01/2016−08/31/2016
地铁系统人流量 HZMetro 80 248 − − 01/01/2019−/26/2019

3.2 实验设置
在实验中, 将所有数据集按照 6:2:2 的比例划分为训练集、验证集和测试集. 使用标准化 Min-Max 方法将
数据归一化至[−1,1], 将处理后的数据输入 MVSTGCN, 其中, 输入数据为基于历史 1h 的交通流量序列, 预测
未来 1h 的交通流量序列. 由于数据集以 5min 为时间间隔聚合, 因此未来 1h 交通流量序列即未来 12 个时间
步长交通流量序列. 本文基于 PyTorch 框架实现了 MVSTGCN 模型, 模型的超参数由验证集的性能决定, 模型
维度 d 设置为 32, 注意力头的数量 h 设置为 8, 学习率 lr 设置为 0.001, 编码器/解码器层数 L 设置为 5.
3.3 评价指标及基准模型
为了验证本文提出 MVSTGCN 的有效性, 在本节中, 我们将其与以下 11 种交通流量预测方法进行比较,
其中, 前 6 种为基准模型, 后 5 种为前沿模型.
(1) HA [15] : 历史均值法, 使用相应历史时期的交通流量平均值来预测下一时间片的交通流量值;
(2) VAR [41] : 向量自回归模型, 高级时间序列预测模型, 能够捕获所有交通序列之间的空间相关性;
(3) SVR [20] : 支持向量回归模型, 利用线性支持向量机实现预测任务;
(4) LSTM [42] : 长短时记忆网络, LSTM 作为较为主流的时间序列预测模型, 是一种特殊的 RNN 模型, 一
定程度上解决了传统 RNN 所存在的梯度爆炸和梯度消失等问题;
(5) DCRNN [29] : 扩散卷积循环神经网络, 使用图上的双向随机游走来捕获空间相关性, 并使用具有预
定采样的编码器-解码器架构来捕获时间相关性, 实现多步交通预测;
(6) STGCN [13] : 时空图卷积网络, 通过集合图卷积和门控时间卷积的时空模块, 有效捕获全面的时空相
关性, 进行时空交通流量预测;
(7) Graph WaveNet [33] : 将自适应邻接矩阵引入图卷积网络捕获动态的空间依赖性, 并使用扩展随机卷
积捕获时间依赖性;
(8) ASTGCN [30] : 基于注意力的时空图卷积网络, 分别使用空间注意和时间注意机制, 建模空间和时间
动态, 在真实公路交通流量数据集上取得较好的效果;
(9) STSGCN [43] : 时空同步图卷积网络, 构建多个局部时空子图模块以同步捕获局部时空依赖性;
(10) ASTGNN [32] : 基于注意力的时空图神经网络, 在时间和空间维度上分别使用时间趋势自注意机制和
动态图卷积实现交通数据动态性建模, 同时考虑了交通数据的周期性和空间异质性;
(11) STFGNN [14] : 时空融合图神经网络, 使用 DTW 算法来构建图, 通过对生成的时空图执行融合操作
来有效学习隐藏的相关性.
为验证提出 MVSTGCN 的有效性, 本文采用平均绝对误差(mean absolute error, MAE)、均方根误差(root
mean square error, RMSE)和平均绝对百分比误差(mean absolute percentage error, MAPE)作为评价指标, 具体
的计算公式如下:
1
N
MAE = ∑ | y − ˆ | (22)
y
N i= 1 i i
1 N
2
RMSE = ∑ (y − y ˆ ) (23)
N i= 1 i i