Page 166 - 《软件学报》2024年第4期

1744 软件学报 2024 年第 35 卷第 4 期

各种对比算法在不同任务上的收敛效果以及 BBT 系列任务的泛化性能(泛化性能只在测试集上测试
当前最优解的性能, 测试集并不会参与到训练过程). 从图 8 中可以看出, GRACE 算法在各任务上均
能够较快地收敛; 从表 3 中展示的各种算法的最终收敛情况, 可以看出 GRACE 可以收敛到高质量解;
• 在运行时间方面, 从表 3 中的平均评估时间可以看出, GRACE 算法能够很好地权衡优化时间和解的
性能, 在使用远少于多保真度优化方法(BOHA, ASHA)运行时间的情况下, 实现高质量的收敛.
(3) 稳健性.
我们设计了针对 GRACE 超参数γ的实验, 通过不同超参数配置下的实验结果说明 GRACE 算法的超参数
稳健性. 超参数γ控制着对批量相似树的分割, 同时间接控制着每次评估使用的批量数. 在算法超参数稳健性
分析部分, 本文通过选取γ的不同取值{1.0,2.0,4.0,5.0,6.0,8.0,10.0,12.0}, 观察 GRACE 的性能变化. 在 SST-2 数
据集和 Housing 数据集上的超参数实验结果分别如图 8(e)、图 8(g)所示. 从图中可以看出: 除了较为极端的(1.0
和 12.0), 其他超参数取值均能取得较好的收敛效果, 这体现了 GRACE 算法的稳健性. 同时可以发现: 尽管在
一定范围的超参数配置下, GRACE 算法在各任务上均能取得较好的收敛效果, 但对于不同的任务, 超参数γ的
最优取值可能有所不同, 这也是未来工作可进一步探索的问题, 即自适应调节γ.
(4) 可理解性.
通过展示 GRACE 算法在优化过程中使用批量数目的动态变化, 我们可以加强对算法行为的理解, 进而
分析算法的行为特征. 同时, 针对不同的批量大小进行实验, 观察算法的性能变化.
通过动态展示优化过程中评估使用的批量数, 进而对算法的内部运行过程进行深入的分析. 在这部分实
验中, 选取了分类任务 SST-2、AG’s News 和回归任务 Housing 进行进一步的分析, 实验结果如图 8(a)~图(c)
所示. 同时, 在超参数实验中, 本文也绘制了 GRACE 在超参数γ不同取值下的评估批量数动态变化图, 如图
8(f)和图 8(h)所示.

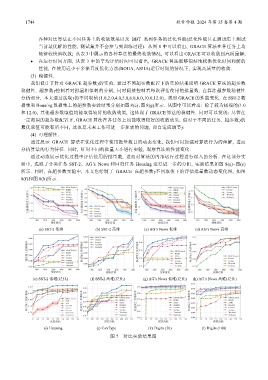
(a) SST-2 低维 (b) SST-2 高维 (c) AG’s News 低维 (d) AG’s News 高维

(e) SST-2 低维(泛化) (f) SST-2 高维(泛化) (g) AG’s News 低维(泛化) (h) AG’s News 高维(泛化)

(i) Housing (j) CovType (k) Digits (50) (l) Digits (100)
图 7 对比实验结果图