Page 139 - 摩擦学学报2025年第5期

第 5 期 许华林, 等: 阶梯螺旋槽端面密封摩擦学性能数值研究 773

力；ρ 为润滑介质液相密度. r = r i e θtanφ (6)
L
针对Jakobsson-Floberg-Olsson (JFO)空化边界条
式中，r 为密封端面内径，θ为转角，φ为螺旋角.
i
件，引入无量纲独立变量ϕ和空化指数F，二者将空化 为方便网格划分并提高计算效率及准确率，本文中
区和全膜区的润滑方程统一，在迭代中自动切换，即 令 Y= cotφln(r /r )−cotφlnr， X=θ+cotφln(r /r )−cotφlnr，
o i
o i
ρ
p− p c
Fϕ = ; = 1+(1− F)ϕ; 通过坐标变换将图2(a)所示曲线边界计算域转换为图2(b)
p ref − p c ρ L
所示的矩形计算域.
®
1 ϕ ⩾ 0
F(r,θ) = (3) 网格划分方式如图2(c)所示，径向采用均匀网格，
0 ϕ < 0
网格数量为N . 周向为非均匀网格，台区和槽区为均
1
式中，ρ为节点处介质气液混合密度. 当ϕ<0时，空化指
匀网格，网格数分别为n 和n ，阶梯处进行网格加密，
1
2
数F=0，此时ρ/ρ <1，该区域为空化区域；当ϕ≥0时， 网格数为n ，网格总数量为N =n +n +3n .
L
3
2
2
3
1
F=1，ρ/ρ =1，该区域为全膜区域. 1.3 数值求解方法
L
内外径处(计算域径向边界)的压力边界条件为 采用控制体积法对式(1)进行离散，如图2(d)所
p i − p c p o − p c 示，剖面线部分是节点P的控制体积，其各边位于各相
ϕ| r= r i = ; ϕ| r= ro = (4)
r o −r i ro −r i
p ref − p c p ref − p c
邻网格节点中间位置，图2(d)中大写字母为网格节点，
计算域圆周方向采用周期性边界条件为 小写字母为相邻网格节点中间位置. 在控制体积内对
∂ϕ ∂ϕ 式(1)中各项进行积分、离散并进行坐标变换后可得节
ϕ| θ=0 = ϕ| θ=2π/N ; | θ=0 = | θ=2π/N (5)
∂θ ∂θ
点P处ϕ值的差分方程，该方程与周围节点ϕ值有关. 采
式中，N为槽数. 用SOR迭代法对离散的代数方程组进行求解，得到独

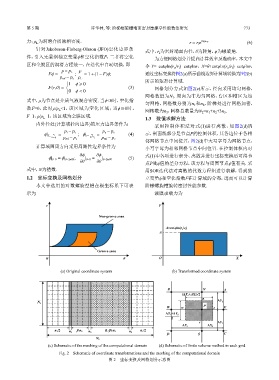
1.2 坐标变换及网格划分 立变量ϕ和空化指数F在计算域的分布，进而可以计算
本文中选用的对数螺旋型槽在极坐标系下可表 阶梯螺旋槽旋转密封性能参数.
示为 液膜承载力为

r Y
Non-groove zone
A=cotφln(r o /r i )
A
Groove zone
O θ O X

(a) Original coordinate system (b) Transformed coordinate system

B N A
(ΔX 1 +ΔX 2 )/2
n
ΔY 2
N 1
W w P e E
————
ΔY 1 +ΔY 2
2
s ΔY 1
ΔX 1 ΔX 2
n 1 /2 n 3 β·n 2 n 3 (1-β)·n 2 n 3 n 1 /2
D S C
N 2
(c) Schematic of the meshing of the computational domain (d) Schematic of finite volume method in each grid
Fig. 2 Schematic of coordinate transformations and the meshing of the computational domain
图 2 坐标变换及网格划分示意图