Page 106 - 《摩擦学学报》2021年第4期

第 4 期 尹露, 等: 交错式扇贝阻尼密封动力特性研究 549

12 图13和图14分别为不同错开角度下直接、交叉刚

11 度随涡动频率变化. 密封腔室并列时(即无错开角度，
Direct damping/(N·s/m) 9 8 f=20 Hz 时，均表现为正直接刚度. 密封腔室错开一定角度使
α=0°)表现为负直接刚度，而密封腔室错开一定角度
10
f=60 Hz
系统静态稳定性显著提升. 随着涡动频率的增加，扇
f=100 Hz
f=180 Hz
7 f=140 Hz 14
f=220 Hz
f=260 Hz C1 C2 C3
Effective damping/(N·s/m) 8
6 12 C4 C5 C6
C1 C2 C3 C4 C5 C6 C7 C8 C9 C7 C8 C9
Seal cavity position 10

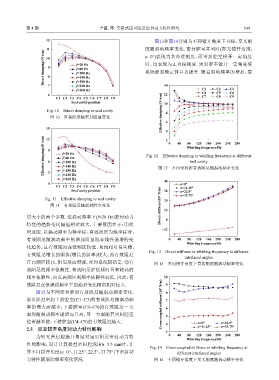
Fig. 10 Direct damping vs seal cavity
图 10 直接阻尼随密封腔室变化 6

15 4 2
Effective damping/(N·s/m) 9 6 f=20 Hz Fig. 12 Effective damping vs whirling frequency at different
12
40
80
280
0
200
160
240
120
Whirling frequency/Hz
f=60 Hz
seal cavity
f=100 Hz
f=140 Hz
f=180 Hz
3
f=220 Hz
f=260 Hz 图 12 不同密封腔有效阻尼随涡动频率变化
48
0 α=0°
C1 C2 C3 C4 C5 C6 C7 C8 C9 α=11.25°
Seal cavity position 36 α=22.5°
α=33.75°
Fig. 11 Effective damping vs seal cavity 24
图 11 有效阻尼随密封腔室变化 Direct stiffness/(10 3 N/m) 12
尼大小的两个参数. 低涡动频率下(f=20 Hz)密封动力 0
特性的趋势变化幅值相对较大，主要原因在于：①阻
−12
尼效应. 以涡动频率为横坐标、有效阻尼为纵坐标时，
有效阻尼随涡动频率的增加而呈现非线性递增的变 0 40 80 120 160 200 240 280
Whirling frequency/Hz
化趋势，且有效阻尼在低频区较低、系统相对易失稳，
Fig. 13 Direct stiffness vs whirling frequency at different
有效阻尼增长的幅值(增长的斜率)较大；而有效阻尼
interlaced angles
在高频区较高，阻尼效应增强，密封系统较稳定. ②有 图 13 不同错开角度下直接刚度随涡动频率变化
效阻尼的频率依赖性. 有效阻尼在低频时具有较高的
频率依赖性，而在高频区则频率依赖性较低. 因此，有 10
效阻尼在低涡动频率下的趋势变化幅值相对较大. 9
图12为不同密封腔的有效阻尼随涡动频率变化. 8
扇贝阻尼密封上游腔室(C1~C3)的有效阻尼随涡动频 7
率的增大而减少；下游腔室(C4~C9)的有效阻尼一方 Cross-coupled stiffness/(10 3 N/m) 6
面均随涡动频率递增而升高，另一方面随着密封腔室 5
位置越靠前，下游腔室(C4~C9)的有效阻尼越大. 4 α=0° α=22.5°

2.3 腔室错开角度对动力特性影响 α=11.25° α=33.75°
3
为研究密封腔错开角度对扇贝阻尼密封动力特 0 40 80 120 160 200 240 280
Whirling frequency/Hz
性的影响，设计计算模型密封腔深度h=3.3 mm时，计
Fig. 14 Cross-coupled stiffness vs whirling frequency at
算不同错开角度(α=0°、11.25°、22.5°、33.75°)下密封动 different interlaced angles
力特性随涡动频率变化情况. 图 14 不同错开角度下交叉刚度随涡动频率变化