Page 105 - 《摩擦学学报》2021年第4期

548 摩 擦 学 学 报 第 41 卷

动的同时，使流体在封闭、独立的扇贝型小腔室内得 接刚度影响较小，越靠近密封腔出口，不同涡动频率
到一定压缩和膨胀，使阻尼更大，有利于改善系统稳 下的直接刚度几乎相等.
定性. 密封腔内压力沿周向分布不均匀，由于转子沿

20
椭圆轨迹持续涡动，当t=0.1 s时，转子正好涡动至靠近
X轴正方向一侧，此时X轴正方向一侧为小间隙，而靠 10
近X轴负方向一侧则为大间隙. 因此，腔体中心靠近 0

X轴正方向一侧出现高压区. Direct stiffness/(10 3 N/m) f=20 Hz
f=60 Hz
−10 f=100 Hz

Velocity/(m/s) f=140 Hz
f=180 Hz
38.000 −20 f=220 Hz
34.200 f=260 Hz
30.400 −30
26.600 C1 C2 C3 C4 C5 C6 C7 C8 C9
Seal cavity position
22.800
Y
19.000
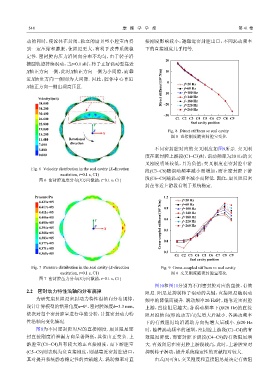
Z Fig. 8 Direct stiffness vs seal cavity
15.200 X 图 8 直接刚度随密封腔室变化
11.400 Rotational
direction
7.600
不同密封腔对应的交叉刚度如图9所示. 交叉刚
3.800
0.000 度在密封腔上游段(C1~C3)时，涡动频率为20 Hz的交
叉刚度明显较低，且为负值；交叉刚度在密封腔中游
Fig. 6 Velocity distribution in the seal cavity (X-direction
段(C3~C6)随涡动频率减小而增加，而在密封腔下游
excitation, t=0.1 s, C1)
段(C6~C9)随涡动频率减小而降低. 因此，扇贝阻尼密
图 6 密封腔速度分布(X方向激励，t=0.1 s，C1)
封在靠近上游段有利于系统稳定.

Pressure/Pa 1.2
4.423e+05 f=20 Hz
f=60 Hz
4.417e+05 0.9 f=100 Hz
4.411e+05 f=140 Hz
4.406e+05 0.6 f=180 Hz
Y
4.400e+05 f=220 Hz
Z Cross-coupled stiffness/(10 3 N/m) f=260 Hz
4.394e+05 X 0.3
4.388e+05
4.383e+05
4.377e+05 0.0
4.371e+05
−0.3
4.365e+05
C1 C2 C3 C4 C5 C6 C7 C8 C9
Seal cavity position
Fig. 7 Pressure distribution in the seal cavity (X-direction Fig. 9 Cross-coupled stiffness vs seal cavity
excitation, t=0.1 s, C1) 图 9 交叉刚度随密封腔室变化
图 7 密封腔压力分布(X方向激励，t=0.1 s，C1)

图10和图11分别为不同密封腔对应的直接、有效
2.2 密封动力特性沿轴向分布规律 阻尼. 阻尼是抑制转子涡动的关键，直接阻尼随涡动
为研究扇贝阻尼密封动力特性沿轴向分布规律， 频率的降低而提升. 涡动频率20 Hz时，越靠近密封腔
设计计算模型的错开角度α=0°、密封腔深度h=3.3 mm， 上游，直接阻尼越大；各涡动频率下(f≠20 Hz)的直接
依次对每个密封腔室进行单独分析，计算密封动力特 阻尼沿轴向(即流动方向)先增大后减小. 各涡动频率
性沿轴向变化情况. 下的有效阻尼均沿流动方向先增大后减小. f≠20 Hz
图8为不同密封腔对应的直接刚度. 扇贝阻尼密 时，随着涡动频率的递增，密封腔上游段(C1~C4)的有
封直接刚度沿泄漏方向显著降低，其值由正变负. 上 效阻尼降低，而密封腔下游段(C4~C9)的有效阻尼增
游腔室(C1~C4)具有较大的正直接刚度，而下游腔室 大. 有效阻尼在密封腔上游段较高，此时，上游腔室对
(C5~C9)则表现为负直接刚度，则越靠近密封腔进口， 抑制转子涡动、提升系统稳定性的贡献相对较大.
其对提升系统静态稳定性的贡献越大. 涡动频率对直 由式(5)可知，交叉刚度和直接阻尼是决定有效阻